��Ŀ����
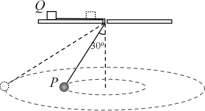
����Ŀ����ͼ��ʾ����ֱƽ������һ�뾶ΪR��![]() �⻬Բ���������ĩ�����㹻����ˮƽ���ƽ�����ӣ�һ����Ϊm��С��P��Բ����������ɾ�ֹ��ʼ�ع���»�����Բ�����ĩ��������Ϊ2m�ľ�ֹС��Q����������ײ��С��P��Q��ˮƽ�����Ķ�Ħ��������Ϊ
�⻬Բ���������ĩ�����㹻����ˮƽ���ƽ�����ӣ�һ����Ϊm��С��P��Բ����������ɾ�ֹ��ʼ�ع���»�����Բ�����ĩ��������Ϊ2m�ľ�ֹС��Q����������ײ��С��P��Q��ˮƽ�����Ķ�Ħ��������Ϊ![]() =0.5���������ٶȴ�СΪg������С��P��Q�����ײΪ��ȫ������ײ����ײʱ�伫�̡���
=0.5���������ٶȴ�СΪg������С��P��Q�����ײΪ��ȫ������ײ����ײʱ�伫�̡���

��1����ײ��˲��С��P��Բ�����ĩ�˵�ѹ����С��
��2��С��P��Q��ֹͣ�˶�����֮��ľ��롣
���𰸡���1��![]() ��2��
��2��![]()
��������
��1��С��P�ɿ�ʼ�»����Ͷ˵Ĺ��̣�![]()
������ײ���̶����غ㣬��е���غ㣬��![]() ��
��
![]() ��
��
������ã�![]() ��
��![]()
С��P������Բ�����ĩ�ˣ�![]()
���![]()
����ţ�ٵ������ɿ�֪����ײ��˲��С��P��Բ�����ĩ�˵�ѹ����СΪ![]()
��2��С��P����Բ��������ص��Ͷ˵��ٶ���Ϊv1�����������������еľ��룺![]()
���![]()
С��Q�����еľ��룺![]()
���![]() ��
��
��С��P��Q��ֹͣ�˶�����֮��ľ���![]() ��
��

��ϰ��ϵ�д�
�����Ŀ