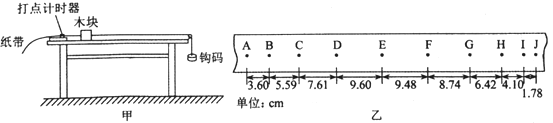
��Ŀ����
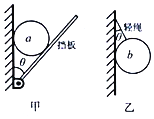
����Ŀ����ͼ��ʾ��������Q���ڴ��й⻬С��ˮƽ�����ϣ�һ������С���������϶���Q�������¶�˩��һ��С��P��С��P��ˮƽ����������Բ���˶���Բ�ڣ�����������ֱ����ļн�Ϊ30o����ʹС��P��ԭˮƽ�������뾶���������Բ���˶�������������ֱ����ļн�Ϊ60o��������Q������С�ס����������Q����ֹ�����һ�������ԭ����Ƚ��� ��
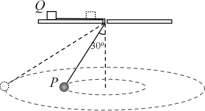
A. С��P�����ٶȸ���
B. С��P�˶������ڸ���
C. С��P����������С֮��Ϊ3 : 1
D. ������Q����Ħ������С֮��Ϊ3 : 1
���𰸡�AC
��������
������Q�����������Ͼ�ֹ������ƽ�������������������֧�����Ƿ�仯����PΪ�о�������ţ�ٵڶ����ɷ���ϸ�ߵ������ı仯���ж�Q�ܵ�����ľ�Ħ�����ı仯����������֪ʶ�ó�С��P�˶��Ľ��ٶȡ����ٶ���ϸ������ֱ����нǵĹ�ϵ�����ж���仯��
A���ϸ������ֱ����ļн�Ϊ�ȣ�ϸ�ߵ�������СΪT��ϸ�ߵij���ΪL����Բ�ĵĸ߶�Ϊh��P��������Բ���˶�ʱ����������ϸ�ߵ������ĺ����ṩ����������ͼ�����У�
![]()
��ã�![]() ������
������![]() Խ�����ٶ�Խ��A��ȷ��
Խ�����ٶ�Խ��A��ȷ��
B��ɹ�ʽ![]() ������С������ڲ��䣬��B����
������С������ڲ��䣬��B����
C�С���������Ϊ��![]() ������������֮��Ϊ��
������������֮��Ϊ��![]() ����C��ȷ��
����C��ȷ��
D�ϸ������T=![]() ����Q����ƽ��������֪��Q�ܵ�����ľ�Ħ��������ϸ�ߵ�������С�����Խ�����Q����Ħ������С֮��Ϊ
����Q����ƽ��������֪��Q�ܵ�����ľ�Ħ��������ϸ�ߵ�������С�����Խ�����Q����Ħ������С֮��Ϊ![]() ����D����
����D����
��ѡ��AC��