��Ŀ����
 ��ͼ��ʾ�������Ϊ30��Ĺ⻬б���ϣ�һ����ϵ��Ϊk1�����ʵ���һ�˹̶��ڹ̶�����C�ϣ���һ������һ����ΪM������A����һ����ϵ��Ϊk2���ᵯ��һ����A����һ����ϸ���ף������˻��ֺ�������ֱ�´���ֱϸ������ʱ������aλ�ã���K2Ϊԭ��״̬���������Ϲ�����Ϊm������Bʱ�����½���b��K1Ϊԭ��״̬��A�ٴ�ƽ�����������B��������A������֮�ȣ����������Ƶľ���hab��
��ͼ��ʾ�������Ϊ30��Ĺ⻬б���ϣ�һ����ϵ��Ϊk1�����ʵ���һ�˹̶��ڹ̶�����C�ϣ���һ������һ����ΪM������A����һ����ϵ��Ϊk2���ᵯ��һ����A����һ����ϸ���ף������˻��ֺ�������ֱ�´���ֱϸ������ʱ������aλ�ã���K2Ϊԭ��״̬���������Ϲ�����Ϊm������Bʱ�����½���b��K1Ϊԭ��״̬��A�ٴ�ƽ�����������B��������A������֮�ȣ����������Ƶľ���hab�������������浯��Ϊ�о������������ƽ���з������m��������Ȼ��δ������ʱ������k1�ܵ���ѹ����С����A��������б�����µķ��������ݺ��˶��������ʱ�õ��ɵ�ѹ��������A�뵲��C�伷ѹ��ǡ��Ϊ��ʱ��A�ܵ�k2����������A������б�����µķ��������ݺ��˶��������ʱ����k2���쳤���������������½��ľ��룮
����⣺�١��Ե���k2Ϊ�о���������ƽ�⣺mg=Mgsin30��
����mg=
Mg
��m=
M
=
�ڡ����ݺ��˶��ɣ�k1ѹ���� x1=
k2�쳤�� x2=
hab=x1+x2=
+
=
+
=
?
�𣺢�����B��������A������֮��
��
���������Ƶľ���habΪ
��
����mg=
| 1 |
| 2 |
��m=
| 1 |
| 2 |
| m |
| M |
| 1 |
| 2 |
�ڡ����ݺ��˶��ɣ�k1ѹ���� x1=
| Mg |
| 2k1 |
k2�쳤�� x2=
| mg |
| k2 |
hab=x1+x2=
| Mg |
| 2k1 |
| Mg |
| k2 |
| Mg |
| 2k1 |
| Mg |
| 2k2 |
| Mg |
| 2 |
| k1+k2 |
| k1k2 |
�𣺢�����B��������A������֮��
| 1 |
| 2 |
���������Ƶľ���habΪ
| Mg(k1+k2) |
| 2k1k2 |
���������ڵ������⣬Ҫ��������ĩ����״̬���ɵı�����������������½��ľ��룬�Ǿ������õ�˼·��

��ϰ��ϵ�д�
�����Ŀ
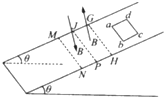 ��ͼ��ʾ�������Ϊ�ȵĹ⻬б���ϣ�������������С��ȡ������෴����ǿ�ų����ų�������б�洹ֱ�����ų��Ŀ���MJ��JG��ΪL��һ������Ϊm������ΪR���߳�ҲΪL�������ε��߿��ɾ�ֹ��ʼ��б���»�����ab�߸�Խ��GH����ų�ʱ���߿�ǡ�����ٶ�v0������ֱ���˶�����ab���»���JP��MN���м�λ��ʱ���߿���ǡ�����ٶ�v������ֱ���˶���������˵����ȷ���ǣ�������
��ͼ��ʾ�������Ϊ�ȵĹ⻬б���ϣ�������������С��ȡ������෴����ǿ�ų����ų�������б�洹ֱ�����ų��Ŀ���MJ��JG��ΪL��һ������Ϊm������ΪR���߳�ҲΪL�������ε��߿��ɾ�ֹ��ʼ��б���»�����ab�߸�Խ��GH����ų�ʱ���߿�ǡ�����ٶ�v0������ֱ���˶�����ab���»���JP��MN���м�λ��ʱ���߿���ǡ�����ٶ�v������ֱ���˶���������˵����ȷ���ǣ�������| A��v=v0 | ||
| B���߿��뿪MN�Ĺ����е�������Ϊadcba | ||
| C����ab�߸�Խ��JPʱ���߿���ٶȵĴ�СΪ3 gsin�� | ||
D����ab�߸�Խ��GH��ab�߸�Խ��MN�����У��߿����������Ϊ2mgLsin��+
|
 ��ͼ��ʾ�������Ϊ��=30���б���ϣ��̶�һ��L=0.25m��ƽ�н������죬�ڵ����϶˽����Դ�ͱ���������Դ�綯��E=12V������r=1.0��һ����m=20g�Ľ�����ab�������촹ֱ���Ӵ����ã�����װ�ô��ڴŸ�ǿ��B=0.80T����ֱ��б�����ϵ���ǿ�ų��У�������������ĵ��費�ƣ������������ǹ⻬�ģ�ȡg=10m/s2��Ҫ���ֽ������ڵ����Ͼ�ֹ����
��ͼ��ʾ�������Ϊ��=30���б���ϣ��̶�һ��L=0.25m��ƽ�н������죬�ڵ����϶˽����Դ�ͱ���������Դ�綯��E=12V������r=1.0��һ����m=20g�Ľ�����ab�������촹ֱ���Ӵ����ã�����װ�ô��ڴŸ�ǿ��B=0.80T����ֱ��б�����ϵ���ǿ�ų��У�������������ĵ��費�ƣ������������ǹ⻬�ģ�ȡg=10m/s2��Ҫ���ֽ������ڵ����Ͼ�ֹ���� ��ͼ��ʾ�������Ϊ�ȵĹ⻬�̶�б���ϣ�����ϵ���ֱ�Ϊk1��k2�������ᵯ��ƽ����б�������ţ�k1���� k2���£�������֮����һ����Ϊm1�����������F��δ֪����б�����ϻ����ƶ�m2���������ɵ��ܳ����������ɵ�ԭ��֮��ʱ��
��ͼ��ʾ�������Ϊ�ȵĹ⻬�̶�б���ϣ�����ϵ���ֱ�Ϊk1��k2�������ᵯ��ƽ����б�������ţ�k1���� k2���£�������֮����һ����Ϊm1�����������F��δ֪����б�����ϻ����ƶ�m2���������ɵ��ܳ����������ɵ�ԭ��֮��ʱ�� ��ͼ��ʾ�������Ϊ30���б���ϣ�����������L=0.5m��ƽ�е��죬����Դ�������������õ��������ڵ����ϣ��ڵ����Ϻ��һ������m=0.2kg�Ľ�����ab����Դ�綯��E=12V������r=0.3�����������뵼������Ħ����Ϊfm=0.6N���ų�����ֱ�������ƽ�棬B=0.8T��������ab�ĵ���Ϊ0.2����������費�ƣ���ʹ�˵Ĺ���ϱ��־�ֹ�������������ĵ����ȡֵ��Χ���gȡ10m/s2��
��ͼ��ʾ�������Ϊ30���б���ϣ�����������L=0.5m��ƽ�е��죬����Դ�������������õ��������ڵ����ϣ��ڵ����Ϻ��һ������m=0.2kg�Ľ�����ab����Դ�綯��E=12V������r=0.3�����������뵼������Ħ����Ϊfm=0.6N���ų�����ֱ�������ƽ�棬B=0.8T��������ab�ĵ���Ϊ0.2����������費�ƣ���ʹ�˵Ĺ���ϱ��־�ֹ�������������ĵ����ȡֵ��Χ���gȡ10m/s2�� ��ͼ��ʾ�������Ϊ30���б���ϣ���A��ˮƽ�׳�һ�����壬����б���ϵ�B�㴦��A��B����������10m���� ȡg=10m/s2����
��ͼ��ʾ�������Ϊ30���б���ϣ���A��ˮƽ�׳�һ�����壬����б���ϵ�B�㴦��A��B����������10m���� ȡg=10m/s2����