题目内容
(15分)如图所示,水平光滑绝缘轨道MN的左端有一固定绝缘挡板,轨道所在空间存在水平向左、E=4×102N/C的匀强电场。一个质量m=0.2kg、带电荷量q=5.0×10-5C的滑块(可视为质点),从轨道上与挡板相距x1=0.2m的P点由静止释放,滑块在电场力作用下向左做匀加速直线运动。当滑块与挡板碰撞后滑块沿轨道向右做匀减速直线运动,运动到与挡板相距x2=0.1m的Q点,滑块第一次速度减为零。若滑块在运动过程中,电荷量始终保持不变,求:
(1)滑块由静止释放时的加速度大小a;
(2)滑块从P点第一次达到挡板时的速度大小v;
(3)滑块与挡板第一次碰撞的过程中损失的机械能ΔE。
(1) 0.1m/s2 (2) 0.2m/s (3) 2×10-3J
解析试题分析:(1)设滑块沿轨道向左做匀加速运动的加速度为a,根据牛顿第二定律有
qE=ma (3分)
代入数据得a=0.1m/s2。 (2分)
(2)滑块从P点运动到挡板处的过程中,由动能定理有
qEx1=mv2/2 (3分)
代入数据有v=0.2m/s。 (2分)
(3)滑块第一次与挡板碰撞过程中损失的机械能等于滑块由P点运动到Q点过程中电场力所做的功,即ΔE=qE(x1-x2)=2×10-3J。 (5分)
考点:本题考查牛顿第二定律和动能定理。

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
(14分)如图所示,在动摩擦因素μ=0.2的水平面AB上,水平恒力F推动质量为m=1kg的物体从A点由静止开始作匀加速直线运动,物体到达B点时撤去F,接着又冲上光滑斜面(设经过B点前后速度大小不变),最高能到达C点。用速度传感器测量物体的瞬时速度,并在表格中记录了部分测量数据。求:(g取10m/s2)
| t/s | 0.0 | 0.2 | 0.4 | … | 2.2 | 2.4 | 2.6 | … |
| v/m?s-1 | 0.0 | 0.4 | 0.8 | … | 3.0 | 2.0 | 1.0 | … |

(1)恒力F 的大小;
(2)在答题纸的坐标上标出记录的数据点,并作v-t图;
(3)若撤去推力F,在A处给物体一个水平向左的初速度v0,恰能使物体运动到C点,求此初速度v0的大小。

 静止在光滑斜面底部的压缩弹簧的顶端此时小球距斜面顶端的高度为
静止在光滑斜面底部的压缩弹簧的顶端此时小球距斜面顶端的高度为 .解除弹簧的锁定后,小球沿斜面向上运动.离开斜面后,达到最高点时(此时
.解除弹簧的锁定后,小球沿斜面向上运动.离开斜面后,达到最高点时(此时 发生弹性碰撞,碰撞后球
发生弹性碰撞,碰撞后球 同一高度,球
同一高度,球 上的
上的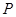 点,
点,  与
与 .已知球
.已知球 ,悬绳长
,悬绳长 ,视两球为质点,重力加速度为
,视两球为质点,重力加速度为 ,不计空气阻力.求:
,不计空气阻力.求:
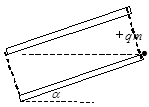
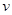 的
的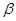 射线,B为金属网,A、B连接在电路上,电源电动势为
射线,B为金属网,A、B连接在电路上,电源电动势为 ,内阻为
,内阻为 ,滑动变阻器总阻值为
,滑动变阻器总阻值为 ,图中滑动变阻器滑片置于中点,A、B间距为d,M为荧光屏(足够大),它紧挨者金属网外侧,已知
,图中滑动变阻器滑片置于中点,A、B间距为d,M为荧光屏(足够大),它紧挨者金属网外侧,已知 ,不计
,不计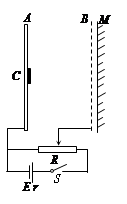


 ,桌面高出地面0.8m,求小球飞出后的落地点距桌边的水平距离。
,桌面高出地面0.8m,求小球飞出后的落地点距桌边的水平距离。