题目内容
如图所示，光滑斜面的倾角为θ=37°，可以看成质点的某物体的质量为m，物体从距离水平面高为h=1.8m的A点由静止开始沿斜面下滑，经过B点后进入粗糙的水平地面（设物体经过B点时速度的大小不变），最后停在C点，已知物体与水平地面的动摩擦因数为μ=0.2，试求出物体到达B点时的速度大小vB和B、C两点间的距离s．（已知sin37°=0.6，g=10m/s2）
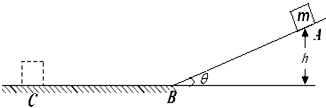
解：在斜面上对物体受力分析，如图所示，设物体在斜面上的加速度大小为a1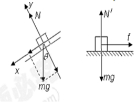
根据牛顿第二定律得，mgsinθ=ma1
解得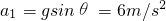
下滑的位移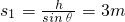
所以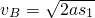
=6m/s．
在粗糙水平面上对物体受力分析，如图所示，设物体的加速度大小为a2
则f=μN=ma2
N′=mg
解得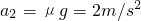
所以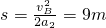
．
答：物体到达B点时的速度大小为6m/s，B、C两点间的距离为9m．
分析：根据牛顿第二定律求出物体下滑的加速度，根据速度位移公式求出物体滑动B点的速度，根据牛顿第二定律求出物体在 水平面上的加速度，结合速度位移公式求出B、C两点间的距离．
点评：本题综合考查了牛顿第二定律和运动学公式，知道加速度是联系力学和运动学的桥梁．
根据牛顿第二定律得，mgsinθ=ma1
解得
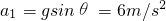
下滑的位移
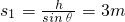
所以
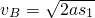=6m/s．在粗糙水平面上对物体受力分析，如图所示，设物体的加速度大小为a2
则f=μN=ma2
N′=mg
解得
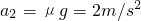
所以
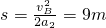．答：物体到达B点时的速度大小为6m/s，B、C两点间的距离为9m．
分析：根据牛顿第二定律求出物体下滑的加速度，根据速度位移公式求出物体滑动B点的速度，根据牛顿第二定律求出物体在 水平面上的加速度，结合速度位移公式求出B、C两点间的距离．
点评：本题综合考查了牛顿第二定律和运动学公式，知道加速度是联系力学和运动学的桥梁．
练习册系列答案
智慧小复习系列答案
相关题目
如图所示，光滑斜面与水平面在B点平滑连接，质量为0.20kg的物体从斜面上的A点由静止开始下滑，经过B点后进入水平面（设经过B点前后速度大小不变），最后停在水平面上的C点．每隔0.20s通过速度传感器测量物体的瞬时速度，下表给出了部分测量数据．取g=10m/s2．
（2011?温州二模）如图所示，光滑绝缘水平面AB与倾角θ=370，长L=6m的绝缘斜面BC在B处圆滑相连，在斜面的C处有一与斜面垂直的弹性绝缘挡板，质量m=0.5kg、所带电荷量q=5x10-5C的绝缘带电滑块置于斜面的中点D，整个空间存在水平向右的匀强电场，场强E=2xlO5N/C，现让滑块以v0=12m/s的速度沿斜面向上运动．设滑块与挡板碰撞前后所带电荷量不变、速度大小不变，滑块和斜面间的动摩擦因数μ=0.1，求：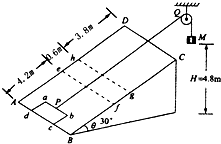
如图所示，光滑矩形斜面ABCD的倾角θ=30°，在其上放置一矩形金属线框abcd，ab的边长l1=1m，bc的边长l2=0.6m，线框的质量m=1kg，电阻R=0.1Ω，线框通过细线绕过定滑轮与重物相连，细线与斜面平行且靠近；重物质量M=2kg，离地面的高度为H=4.8m；斜面上efgh区域是有界匀强磁场，方向垂直于斜面向上；已知AB到ef的距离为S1=4.2m，ef到gh的距离S2=0.6m，gh到CD的距离为S3=3.8m，取g=10m/s2；现让线框从静止开始运动（开始时刻，cd与AB边重合），发现线框匀速穿过匀强磁场区域，求：