题目内容
 如图所示,一根水平光滑的绝缘直槽轨连接一个竖直放置的半径为R=0.50m的绝缘光滑槽轨.槽轨处在垂直纸面向外的匀强磁场中,磁感应强度B=0.50T.有一个质量m=0.10g,带电量为q=+1.6×10-3C的小球在水平轨道上向右运动.若小球恰好能通过最高点,重力加速度g=10m/s2.试求:
如图所示,一根水平光滑的绝缘直槽轨连接一个竖直放置的半径为R=0.50m的绝缘光滑槽轨.槽轨处在垂直纸面向外的匀强磁场中,磁感应强度B=0.50T.有一个质量m=0.10g,带电量为q=+1.6×10-3C的小球在水平轨道上向右运动.若小球恰好能通过最高点,重力加速度g=10m/s2.试求:(1)小球在最高点所受的洛伦兹力F;
(2)小球的初速度v0.
分析:(1)小球恰好通过最高点时,轨道对球无作用力,向心力等于重力和洛伦兹力的合力,由F向=m
,可知在最高点时的速度和受到的洛伦兹力.
(2)从水平轨道到最高点的过程中,只有重力做功,由机械能守恒可得知小球的初速度.
| v2 |
| R |
(2)从水平轨道到最高点的过程中,只有重力做功,由机械能守恒可得知小球的初速度.
解答:解析:(1)设小球在最高点的速度为v,则小球在最高点所受洛伦兹力为:
F=qvB…①
方向竖直向上;由于小球恰好能通过最高点,故小球在最高点由洛伦兹力和重力共同提供向心力,即:
mg-F=
…②
①②两式联立得:v=1m/s,F=8×10-4N
(2)由于无摩擦力,且洛伦兹力不做功,所以小球在运动过程中机械能守恒,由机械能守恒定律可得:
m
=mgh+
mv2…③
其中h=2R…④
解得:v0=
m/s
答:(1)小球在最高点所受的洛伦兹力8×10-4N;
(2)小球的初速度v0为
m/s
F=qvB…①
方向竖直向上;由于小球恰好能通过最高点,故小球在最高点由洛伦兹力和重力共同提供向心力,即:
mg-F=
| mv2 |
| R |
①②两式联立得:v=1m/s,F=8×10-4N
(2)由于无摩擦力,且洛伦兹力不做功,所以小球在运动过程中机械能守恒,由机械能守恒定律可得:
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
其中h=2R…④
解得:v0=
| 21 |
答:(1)小球在最高点所受的洛伦兹力8×10-4N;
(2)小球的初速度v0为
| 21 |
点评:解答该题要挖掘出恰能通过圆形轨道的最高点所隐藏的隐含条件,就是对轨道无压力,该题在此时提供向心力的是重力和洛伦兹力的合力,这是解决此题的关键.

练习册系列答案
相关题目
 (2010?南平模拟)如图所示,在距水平地面高为0.4m处,水平固定一根长直光滑杆,杆上P处固定一定滑轮,滑轮可绕水平轴无摩擦转动,在P点的右边,杆上套一质量m=3kg的滑块A.半径R=0.3m的光滑半圆形轨道竖直地固定在地面上,其圆心O在P点的正下方,在轨道上套有一质量m=3kg的小球B.用一条不可伸长的柔软细绳,通过定滑轮将两小球连接起来.杆和半圆形轨道在同一竖直面内,滑块和小球均可看作质点,且不计滑轮大小的影响.现给滑块A施加一个水平向右、大小为60N的恒力F,则:
(2010?南平模拟)如图所示,在距水平地面高为0.4m处,水平固定一根长直光滑杆,杆上P处固定一定滑轮,滑轮可绕水平轴无摩擦转动,在P点的右边,杆上套一质量m=3kg的滑块A.半径R=0.3m的光滑半圆形轨道竖直地固定在地面上,其圆心O在P点的正下方,在轨道上套有一质量m=3kg的小球B.用一条不可伸长的柔软细绳,通过定滑轮将两小球连接起来.杆和半圆形轨道在同一竖直面内,滑块和小球均可看作质点,且不计滑轮大小的影响.现给滑块A施加一个水平向右、大小为60N的恒力F,则: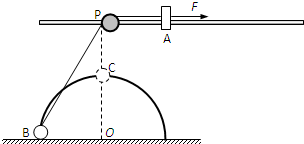 (2011?上海模拟)如图所示,在距水平地面高为H=0.4m处,水平固定一根长直光滑杆,杆上P处固定一定滑轮,滑轮可绕水平轴无摩擦转动,在P点的右边,杆上套一质量m=3kg的滑块A.半径R=0.3m的光滑半圆形轨道竖直地固定在地面上,其圆心O在P点的正下方,在轨道上套有一质量m=3kg的小球B.用一条不可伸长的柔软细绳,通过定滑轮将两小球连接起来.杆和半圆形轨道在同一竖直面内,滑块和小球均可看作质点,且不计滑轮大小的影响.现给滑块A施加一个水平向右、大小为60N的恒力F,则:
(2011?上海模拟)如图所示,在距水平地面高为H=0.4m处,水平固定一根长直光滑杆,杆上P处固定一定滑轮,滑轮可绕水平轴无摩擦转动,在P点的右边,杆上套一质量m=3kg的滑块A.半径R=0.3m的光滑半圆形轨道竖直地固定在地面上,其圆心O在P点的正下方,在轨道上套有一质量m=3kg的小球B.用一条不可伸长的柔软细绳,通过定滑轮将两小球连接起来.杆和半圆形轨道在同一竖直面内,滑块和小球均可看作质点,且不计滑轮大小的影响.现给滑块A施加一个水平向右、大小为60N的恒力F,则: (2013?安庆三模)如图所示,两根等长且不可伸长的细线结于O点,A端固定在水平杆上,B端系在轻质圆环(不计重力)上,圆环套在竖直光滑杆上,C端挂一重物,重物质量为m.开始时用手握住轻圆环,使其紧靠D端,且AD=OA,当重物静止时如图所示.现释放圆环,圆环在竖直光滑杆上自由滑动,当重物再次静止时OA绳拉力为FA,OB绳拉力为FB,则( )
(2013?安庆三模)如图所示,两根等长且不可伸长的细线结于O点,A端固定在水平杆上,B端系在轻质圆环(不计重力)上,圆环套在竖直光滑杆上,C端挂一重物,重物质量为m.开始时用手握住轻圆环,使其紧靠D端,且AD=OA,当重物静止时如图所示.现释放圆环,圆环在竖直光滑杆上自由滑动,当重物再次静止时OA绳拉力为FA,OB绳拉力为FB,则( ) 如图所示,在距水平地面高为0.4m处,水平固定一根长直光滑杆,在杆上P点固定一定滑轮,滑轮可绕水平轴无摩擦转动,在P点的右边,杆上套有一质量m=2kg小球A.半径R=0.3m的光滑半圆形细轨道,竖直地固定在地面上,其圆心O在P点的正下方,在轨道上套有一质量也为m=2kg的小球B.用一条不可伸长的柔软细绳,通过定滑轮将两小球连接起来.杆和半圆形轨道在同一竖直面内,两小球均可看作质点,且不计滑轮大小的影响,g取10m/s2.现给小球A一个水平向右的恒力F=55N.求:(1)把小球B从地面拉到P点正下方C点过程中,力F做的功;(2)小球B运动到C处时的速度大小;(3)小球B被拉到离地多高时与小球A速度大小相等.
如图所示,在距水平地面高为0.4m处,水平固定一根长直光滑杆,在杆上P点固定一定滑轮,滑轮可绕水平轴无摩擦转动,在P点的右边,杆上套有一质量m=2kg小球A.半径R=0.3m的光滑半圆形细轨道,竖直地固定在地面上,其圆心O在P点的正下方,在轨道上套有一质量也为m=2kg的小球B.用一条不可伸长的柔软细绳,通过定滑轮将两小球连接起来.杆和半圆形轨道在同一竖直面内,两小球均可看作质点,且不计滑轮大小的影响,g取10m/s2.现给小球A一个水平向右的恒力F=55N.求:(1)把小球B从地面拉到P点正下方C点过程中,力F做的功;(2)小球B运动到C处时的速度大小;(3)小球B被拉到离地多高时与小球A速度大小相等. 如图所示,一根光滑杆弯成半圆形,上穿一质量为m的小球,用细绳系于一端.现测得绳与水平面的夹角为30°,则细绳对小球的拉力为
如图所示,一根光滑杆弯成半圆形,上穿一质量为m的小球,用细绳系于一端.现测得绳与水平面的夹角为30°,则细绳对小球的拉力为