题目内容
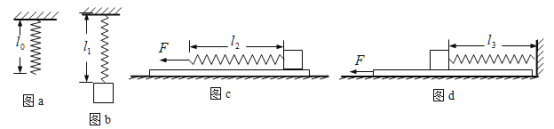
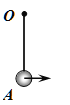
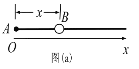
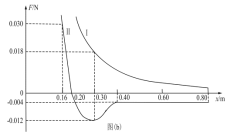
【题目】如图(a),长度L=0.8m的光滑杆左端固定一带正电的点电荷A,其电荷量Q=![]() ;一质量m=0.02kg,带电量为q的小球B套在杆上。将杆沿水平方向固定于某非均匀外电场中,以杆左端为原点,沿杆向右为x轴正方向建立坐标系。点电荷A对小球B的作用力随B位置x的变化关系如图(b)中曲线I所示,小球B所受水平方向的合力随B位置x的变化关系如图(b)中曲线II所示,其中曲线II在0.16≤x≤0.20和x≥0.40范围可近似看作直线。求:(静电力常量
;一质量m=0.02kg,带电量为q的小球B套在杆上。将杆沿水平方向固定于某非均匀外电场中,以杆左端为原点,沿杆向右为x轴正方向建立坐标系。点电荷A对小球B的作用力随B位置x的变化关系如图(b)中曲线I所示,小球B所受水平方向的合力随B位置x的变化关系如图(b)中曲线II所示,其中曲线II在0.16≤x≤0.20和x≥0.40范围可近似看作直线。求:(静电力常量![]() )
)
(1)小球B所带电量q;
(2)非均匀外电场在x=0.3m处沿细杆方向的电场强度大小E;
(3)在合电场中,x=0.4m与x=0.6m之间的电势差U。
(4)已知小球在x=0.2m处获得v=0.4m/s的初速度时,最远可以运动到x=0.4m。若小球在x=0.16m处受到方向向右,大小为0.04N的恒力作用后,由静止开始运动,为使小球能离开细杆,恒力作用的最小距离s是多少?
【答案】(1)![]() (2)
(2)![]() (3)800 V (4)0.065 m
(3)800 V (4)0.065 m
【解析】(1)由图可知,当x=0.3m时,![]()
因此![]() 。
。
(2)设在x=0.3m处点电荷与小球间作用力为F2,F合=F2+qE
因此![]()
电场在x=0.3m处沿细杆方向的电场强度大小为3![]()
![]() ,方向水平向左。
,方向水平向左。
(3)根据图像可知在x=0.4m与x=0.6m之间合力做功大小W合=0.004×0.2 J=8×10-4J
由qU=W合可得![]()
(4)由图可知小球从x=0.16m到x=0.2m处,电场力做功![]()
小球从![]() 到
到![]() 处,电场力做功
处,电场力做功![]() =
=![]()
![]() =
=![]()
![]()
由图可知小球从![]() 到
到![]() 处,电场力做功
处,电场力做功![]() =-0.004×0.4 J=
=-0.004×0.4 J=![]()
![]()
由动能定理![]() +
+![]() +
+![]() +
+![]() =0
=0
解得![]() =
=![]()

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目