题目内容
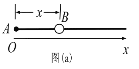
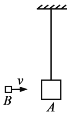
【题目】如图所示,一根长为L=0.2m的刚性轻绳,一端固定在O点,另一端连接一个质量为m的小球,当球自由悬挂时,球处在最低点A点,此时给球一个水平初速度v0让它运动起来,忽略空气阻力,重力加速度![]() 。
。
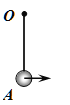
(1)要保证小球在运动过程中绳子始终不松弛,求v0满足的条件;
(2)若小球在A点获得的水平初速度![]() ,试确定小球能上升的最大高度。
,试确定小球能上升的最大高度。
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]()
【解析】试题分析:(1)要保证小球在运动过程中绳子始终不松弛,可以使小球做完整的圆周运动,也可以使小球上升到低于O点的高度后就下落。
①当小球刚好做完整的圆周运动时,在最高点重力提供向心力,有![]()
从最低点到最高点,重力做负功,根据动能定理有![]()
可得小球的初速度![]()
②小球恰好能运动到O点等高的位置时,根据动能定理有![]()
可得小球的初速度![]()
由上分析可知,小球的初速度应![]() 或
或![]()
(2)若小球在A点获得的水平初速度![]() ,则小球不能上升到最高点,设小球上升到高于圆心O的某个位置时,绳子恰好要松弛,此时绳子与竖直方向夹角为
,则小球不能上升到最高点,设小球上升到高于圆心O的某个位置时,绳子恰好要松弛,此时绳子与竖直方向夹角为![]() ,小球只受重力,速度为
,小球只受重力,速度为![]() 。
。
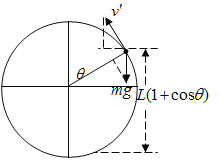
重力沿半径方向的分力提供向心力,有![]()
由几何关系可知,此过程小球上升高度![]()
根据动能定理有![]()
解得:此时小球速度![]() ,
,![]()
此后小球以速度![]() 做斜抛运动,在最高点时竖直方向速度为零,水平方向速度为
做斜抛运动,在最高点时竖直方向速度为零,水平方向速度为![]() ,
,
从最低点到最高点,根据动能定理有:![]()
则小球上升最大高度: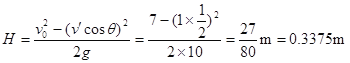
或:由上可知![]() ,
,![]() 。此后小球以速度
。此后小球以速度![]() 做斜抛运动,竖直方向速度为
做斜抛运动,竖直方向速度为![]() 。上升到最高点竖直方向减为零,由
。上升到最高点竖直方向减为零,由![]() 可得,小球继续上升的高度
可得,小球继续上升的高度![]() 。故小球上升最大高度:
。故小球上升最大高度: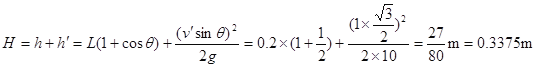 。
。

练习册系列答案
相关题目