题目内容
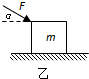
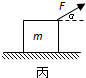
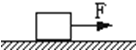
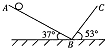
如图所示,地面上放一木箱,质量为40kg,用与水平方向成370角,大小为100N的力推木箱,恰好使木箱匀速前进.若用大小为100N,方向与水平成370角的力斜向上方拉木箱,木箱加速运动(g取10m/s2,sin37°=0.6,cos37°=0.8))求:
(1)木箱与地面的动摩擦因素.
(2)木箱加速运动时的加速度大小.

(1)木箱与地面的动摩擦因素.
(2)木箱加速运动时的加速度大小.

(1)以木箱为研究对象,因为物体匀速运动,物体的受力如右图所示.故根据平衡条件有:
FN-mg-Fsin37°=0
Fcos37°-Ff=0
又 Ff=μFN
解得:μ=
=
=0.17;
(2)当F斜向上拉时,物体的受力如右图所示.根据牛顿第二定律有:
FN′+Fsin37°-mg=0
Fcos37°-Ff=ma
又 Ff′=μFN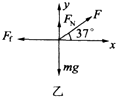 ′
′
解得:a=
[Fcos37°-μ(mg-Fsin37°)]
=
×[100×0.8-0.17×(400-100×0.6)]
=0.56m/s2;
答:
(1)木箱与地面的动摩擦因数为0.17.
(2)木箱加速运动时的加速度大小为0.56m/s2.

FN-mg-Fsin37°=0
Fcos37°-Ff=0
又 Ff=μFN
解得:μ=
| Fcos37° |
| mg+Fsin37° |
| 100×0.8 |
| 400+100×0.6 |
(2)当F斜向上拉时,物体的受力如右图所示.根据牛顿第二定律有:
FN′+Fsin37°-mg=0
Fcos37°-Ff=ma
又 Ff′=μFN
 ′
′解得:a=
| 1 |
| m |
=
| 1 |
| 40 |
=0.56m/s2;
答:
(1)木箱与地面的动摩擦因数为0.17.
(2)木箱加速运动时的加速度大小为0.56m/s2.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目