题目内容
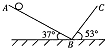
如图所示，两个光滑斜面AB、BC分别与水平面成37°角和53°角，在B处通过光滑小圆弧相连，已知sin37°=0.6，sin53°=0.8．现在在斜面AB上某一高处无初速度释放一个小球，小球从释放到在斜面BC上上升到最高点的过程中，关于小球在斜面AB及BC上的运动，下列说法中正确的是（ ）
| A．运动的时间相等 | B．运动的时间之比为4：3 |
| C．运动的时间之比为3：4 | D．加速度大小之比为4：3 |
根据牛顿第二定律，在AB面上的加速度为：a=
=gsin37°=0.6g
在BC面上的加速度为：a′=gsin53°=0.8g
故加速度之比为a：a′=3：4，故D错误；
根据匀变速直线运动的速度时间公式有：at=a′t′
得：
=
=
，故B正确，AC错误；
故选：B．
| mgsin37° |
| m |
在BC面上的加速度为：a′=gsin53°=0.8g
故加速度之比为a：a′=3：4，故D错误；
根据匀变速直线运动的速度时间公式有：at=a′t′
得：
| t |
| t′ |
| a′ |
| a |
| 4 |
| 3 |
故选：B．
练习册系列答案
相关题目
