题目内容
(12分)一个平板小车置于光滑水平面上,其右端恰好和一个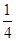 光滑圆弧轨道AB的底端等高对接,如图所示.已知小车质量M=3.0 kg,长L=2.06 m,圆弧轨道半径R=0.8 m.现将一质量m=1.0 kg的小滑块,由轨道顶端A点无初速释放,滑块滑到B端后冲上小车.滑块与小车上表面间的动摩擦因数μ=0.3 (取g=10 m/s2),求:
光滑圆弧轨道AB的底端等高对接,如图所示.已知小车质量M=3.0 kg,长L=2.06 m,圆弧轨道半径R=0.8 m.现将一质量m=1.0 kg的小滑块,由轨道顶端A点无初速释放,滑块滑到B端后冲上小车.滑块与小车上表面间的动摩擦因数μ=0.3 (取g=10 m/s2),求:
(1)滑块到达B端时,轨道对它支持力的大小
(2)小车运动1.5 s时,车右端距轨道B端的距离
(3)滑块与车面间由于摩擦而产生的内能
 光滑圆弧轨道AB的底端等高对接,如图所示.已知小车质量M=3.0 kg,长L=2.06 m,圆弧轨道半径R=0.8 m.现将一质量m=1.0 kg的小滑块,由轨道顶端A点无初速释放,滑块滑到B端后冲上小车.滑块与小车上表面间的动摩擦因数μ=0.3 (取g=10 m/s2),求:
光滑圆弧轨道AB的底端等高对接,如图所示.已知小车质量M=3.0 kg,长L=2.06 m,圆弧轨道半径R=0.8 m.现将一质量m=1.0 kg的小滑块,由轨道顶端A点无初速释放,滑块滑到B端后冲上小车.滑块与小车上表面间的动摩擦因数μ=0.3 (取g=10 m/s2),求:
(1)滑块到达B端时,轨道对它支持力的大小
(2)小车运动1.5 s时,车右端距轨道B端的距离
(3)滑块与车面间由于摩擦而产生的内能
(1)30 N(2)1 m(3)6 J
(1)滑块从A端下滑到B端,由动能定理得mgR= mv02-0 (2分)
mv02-0 (2分)
在B点由牛顿第二定律得FN-mg= (2分)
(2分)
解得轨道对滑块的支持力FN=3 mg=30 N (1分)
(2)滑块滑上小车后,由牛顿第二定律
对滑块:-μmg=ma1,得a1=-3 m/s2 (1分)
对小车:μmg=Ma2,得a2=1 m/s2 (1分)
设经时间t后两者达到共同速度,则有v0+a1t=a2t
解得t=1 s
由于t=1 s<1.5 s,
故1 s后小车和滑块一起匀速运动,速度v=1 m/s (1分)
因此,1.5 s时小车右端距轨道B端的距离为s= a2t2+v(1.5-t)=1 m (1分)
a2t2+v(1.5-t)=1 m (1分)
(3)滑块相对小车滑动的距离为Δs= t-
t- t=2 m (1分)
t=2 m (1分)
所以产生的内能Q=μmgΔs=6 J (2分)
本题考查对牛顿第二定律和圆周运动的应用,由A到B时应用动能定理列式可求出物体在B点的速度,在B点合力提供向心力,根据牛顿第二定律可求出此时物体受到的支持力,物体滑上小车后所受摩擦力向右,物体向左做匀减速直线运动,反之小车向左最匀加速直线运动,当两者达到共同速度时求出时间为1s,所以在1.5s时刻两者以匀速运动,根据小车匀加速和匀速两个过程求解车右端距轨道B端的距离
 mv02-0 (2分)
mv02-0 (2分)在B点由牛顿第二定律得FN-mg=
 (2分)
(2分)解得轨道对滑块的支持力FN=3 mg=30 N (1分)
(2)滑块滑上小车后,由牛顿第二定律
对滑块:-μmg=ma1,得a1=-3 m/s2 (1分)
对小车:μmg=Ma2,得a2=1 m/s2 (1分)
设经时间t后两者达到共同速度,则有v0+a1t=a2t
解得t=1 s
由于t=1 s<1.5 s,
故1 s后小车和滑块一起匀速运动,速度v=1 m/s (1分)
因此,1.5 s时小车右端距轨道B端的距离为s=
 a2t2+v(1.5-t)=1 m (1分)
a2t2+v(1.5-t)=1 m (1分)(3)滑块相对小车滑动的距离为Δs=
 t-
t- t=2 m (1分)
t=2 m (1分)所以产生的内能Q=μmgΔs=6 J (2分)
本题考查对牛顿第二定律和圆周运动的应用,由A到B时应用动能定理列式可求出物体在B点的速度,在B点合力提供向心力,根据牛顿第二定律可求出此时物体受到的支持力,物体滑上小车后所受摩擦力向右,物体向左做匀减速直线运动,反之小车向左最匀加速直线运动,当两者达到共同速度时求出时间为1s,所以在1.5s时刻两者以匀速运动,根据小车匀加速和匀速两个过程求解车右端距轨道B端的距离

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
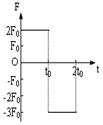
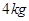 的物体在一恒定水平外力
的物体在一恒定水平外力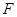 作用下,沿水平面作直线运动,其速度与时间关系图像如图所示.
作用下,沿水平面作直线运动,其速度与时间关系图像如图所示.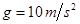 ,试求:
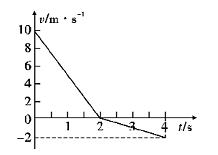
,试求: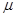 .
.


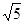 m/s
m/s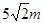

 μg
μg