题目内容
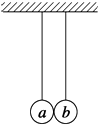
【题目】某小组用如图所示的装置验证动量守恒定律．装置固定在水平面上，圆弧形轨道下端切线水平．两球半径相同，两球与水平面的动摩擦因数相同．实验时，先测出A、B两球的质量mA、mB ， 让球A多次从圆弧形轨道上某一位置由静止释放，记下其在水平面上滑行距离的平均值x0 ， 然后把球B静置于轨道下端水平部分，并将A从轨道上同一位置由静止释放，并与B相碰，重复多次．
①为确保实验中球A不反向运动，则mA、mB应满足的关系是；
②写出实验中还需要测量的物理量及符号：；
③若碰撞前后动量守恒，写出动量守恒的表达式：；
④取mA=2mB ， x0=1m，且A、B间为完全弹性碰撞，则B球滑行的距离为 ．
【答案】mA＞mB；碰撞后A、B球在水平面滑行的距离：xA、xB；mA 
=mA 
+mB 
；
m
【解析】解：①为防止两球碰撞后入射球反弹，入射球的质量应大于被碰球的质量，即：mA＞mB；②碰撞后两球做减速运动，设碰撞后的速度为：vA、vB，
由动能定理得：﹣μmAgx0=0﹣ 
mAv02，v0= 
，
﹣μmAgxA=0﹣ mAvA2，vA= 
，
﹣μmBgxB=0﹣ mBvB2，vB= 
，
如果碰撞过程动量守恒，则：mAv0=mAvA+mBvB，
即：mA =mA +mB ，
整理得：mA =mA +mB ，实验需要测量碰撞后A、B球在水平面滑行的距离：xA、xB．③由②可知，若碰撞前后动量守恒，写出动量守恒的表达式为：
mA =mA +mB ．④如果碰撞过程是完全弹性碰撞，碰撞过程系统动量守恒，以向右为正方向，由动量守恒定律得：
mA =mA +mB ，
由机械能守恒定律得： mA（ ）2= mA（ ）2+ mB（ ）2，
已知：mA=2mB，x0=1m，
解得：xB= m；
所以答案是：①mA＞mB；②碰撞后A、B球在水平面滑行的距离：xA、xB；③mA =mA +mB ；④ m．
