题目内容
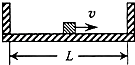
【题目】如图所示，大小相同的摆球a和b的质量分别为m和3m，摆长相同，并排悬挂，平衡时两球刚好接触，现将摆球a向左边拉开一小角度后释放，若两球的碰撞是弹性的，下列判断中正确的是（ ）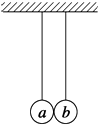
A.第一次碰撞后的瞬间，两球的速度大小不相等
B.第一次碰撞后的瞬间，两球的动量大小相等
C.第一次碰撞后，两球的最大摆角不相同
D.发生第二次碰撞时，两球在各自的平衡位置
【答案】D
【解析】解：A、两球在碰撞前后，水平方向不受外力，故水平方向两球组成的系统动量守恒，取向右为正方向，由动量守恒定律有：
mv0=mv1+3mv2，
两球碰撞是弹性的，故机械能守恒，即为：
mv02= mv12+ 3mv22，
解两式得：v1=﹣ 
，v2= ，
可见第一次碰撞后的瞬间，两球的速度大小相等，方向相反，故A错误；
B、由前面分析知两球速度大小相等，因两球质量不相等，故两球碰后的动量大小不相等，故B错误；
C、两球碰后上摆过程，机械能守恒，故上升的最大高度相等，摆长也相等，故两球碰后的最大摆角相同，故C错误；
D、第一次碰撞后，二者都做单摆运动，由于二者的摆长相同，所以二者单摆的周期也是相等的，所以再经过半个周期后回到平衡位置，然后在平衡位置发生第二次碰撞，故D正确．
故选：D
两球碰撞过程中动量守恒、机械能守恒，由动量守恒与机械能守恒定律列方程，求出碰后的速度，然后答题．
由单摆的周期公式判断回到平衡位置的时间关系．
练习册系列答案
相关题目
