题目内容
一条不可伸长的轻绳跨过质量可忽赂不计的定滑轮,绳的一端系一质量M=15kg的重物,重物静止于地面上,有一质量m=10kg的猴子,从绳的另一端沿绳向上爬,不计滑轮摩擦.在重物不离开地面的条件下,猴子向上爬的最大加速度为:( )
| A.25m/s2 | B.5m/s2 | C.10m/s2 | D.15m/s2 |
B
解析试题分析:分别对重物和猴子受力分析,如下图,由于重物静止在地面,因此,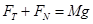 ,对猴子,由牛顿第二定律,
,对猴子,由牛顿第二定律, ,当绳的拉力最大时,加速度
,当绳的拉力最大时,加速度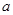 最大,绳的最大拉力
最大,绳的最大拉力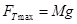 ,解得猴子的最大加速度
,解得猴子的最大加速度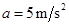 ,所以正确选项为B。
,所以正确选项为B。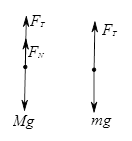
考点:本题考查了受力分析和牛顿运动定律的应用。

如图所示,小球在竖直放置的光滑圆形管道内做圆周运动,内侧壁半径为R,小球半径为r,则下列说法正确的是( )
A.小球通过最高点时的最小速度 |
B.小球通过最高点时的最小速度 |
| C.小球在水平线ab以下的管道中运动时,内侧管壁对小球一定无作用力 |
| D.小球在水平线ab以上的管道中运动时,外侧管壁对小球一定有作用力 |
铁路转弯处的弯道半径r是根据地形决定的.弯道处要求外轨比内轨高,其内外轨高度差h的设计不仅与r有关,还与火车在弯道上的行驶速率v有关.下列说法正确的是
| A.v一定时,r越大则要求h越大 |
| B.v一定时,r越小则要求h越大 |
| C.r一定时,v越大则要求h越大 |
| D.r一定时,v越小则要求h越大 |
雨点从高空由静止下落,在下落过程中,受到的阻力与雨点下落的速度成正比,图中能正确反映雨点下落运动情景的是( )
| A.①② | B.②③ | C.①④ | D.①③ |
如图所示,直杆AB与水平面成α角固定,在杆上套一质量为m的小滑块,杆底端B点处有一弹性挡板,杆与板面垂直,滑块与挡板碰撞后原速率返回.现将滑块拉到A点由静止释放,与挡板第一次碰撞后恰好能上升到AB的中点,设重力加速度为g,由此可以确定
| A.滑块下滑和上滑过程加速度的大小a1、a2 |
| B.滑块最终所处的位置 |
| C.滑块与杆之间动摩擦因数μ |
| D.滑块第k次与挡板碰撞后速度vk |
如图所示,小车的质量为M,人的质量为m,人用恒力F拉绳,若人与车保持相对静止,且地面为光滑的,又不计滑轮与绳的质量,则车对人的摩擦力可能是:
| A.0 |
B. ,方向向右 ,方向向右 |
C. ,方向向左 ,方向向左 |
D. ,方向向右 ,方向向右 |
如图所示,在光滑水平面上有甲、乙两木块,质量分别为m1和m2,中间用一原长为L、劲度系数为k的轻质弹簧连接起来,现用一水平力F向左推木块乙,当两木块一起匀加速运动时,两木块之间的距离是 ( ) 
A. | B. |
C. | D. |
如图所示,质量为M的半圆形轨道槽放置在水平地面上,槽内壁光滑.质量为m的小物体从槽的左侧顶端由静止开始下滑到右侧最高点的过程中,轨道槽始终静止,则该整个过程中 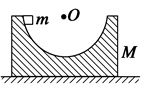
| A.地面对轨道槽的最小压力为(M+m)g |
| B.地面对轨道槽的最大压力为(M+2m)g |
| C.地面对轨道槽的摩擦力始终为零 |
| D.地面对轨道槽的摩擦力方向先向右后向左 |




