Question

【题目】如图，两条间距为L的平行金属导轨位于同一水平面(纸面)内，其左端接一阻值为R的电阻；一金属棒垂直放置在两导轨上；在MN左侧面积为S的圆形区域中存在垂直于纸面向里的均匀磁场，磁感应强度大小B随时间t的变化关系为B=kt，式中k为常量，且k>0；在MN右侧区域存在一与导轨垂直、磁感应强度大小为B0、方向垂直纸面向里的匀强磁场。t=0时刻，金属棒从MN处开始，在水平拉力F作用下以速度v0向右匀速运动。金属棒与导轨的电阻及摩擦均可忽略。则

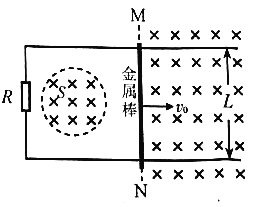
A. 在t时刻穿过回路的总磁通量为 B0Lv0t

B. 电阻R上的电流为恒定电流

C. 在时间△t内流过电阻的电荷量为△t

D. 金属棒所受的水平拉力F随时间均匀增大

Answer 1

【答案】BC

【解析】

A、根据题意可知，MN左边的磁场方向与右边的磁场方向相同，那么总磁通量即为两种情况磁通量之和，则在时刻t穿过回路的总磁通量为Φ＝Φ1+Φ2＝ktS+B0v0tl＝ktS+B0lv0t，故A错误；

B、根据法拉第电磁感应定律得E，结合闭合电路欧姆定律得 I=kS+B0lv0，故通过电阻R上的电流为恒定电流

C、△t时间内通过电阻的电量为q＝I△t，故C正确。

D、金属棒所受的安培力大小FA＝B0Il；根据平衡条件得，水平恒力大小等于安培力大小，即为F。故外力F是一个恒量，故D错误。