题目内容
【题目】如图所示，在xoy平面内，有一以坐标原点O为圆心、R为半径的圆形区圆周与坐标轴分别交于a、b、c、d点。x轴下方圆弧bd与b′d′是两个半圆形同心圆弧，bd和b′d′之间的区域内分布着辐射状的电场，电场方向指向原点O，其间的电势差为U；x轴上方圆周外区域，存在着上边界为y=2R的垂直纸面向里的足够大匀强磁场，圆周内无磁场。圆弧b′d′上均匀分布着质量为m、电荷量为q的带正电粒子，它们被辐射状的电场由静止加速后通过坐标原点O，并进入磁场。不计粒子的重力以及粒子之间的相互作用，不考虑粒子从磁场返回圆形区域边界后的运动。
(1)粒子经电场加速后，在半径为R的圆形区域内运动的时间为多大?
(2)若从a点进入磁场的粒子不能从磁场上边界射出磁场，则磁感应强度应满足什么条件?
(3要使粒子能够垂直于磁场上边界射出磁场，求磁场的磁感应强度的最大值B0；并求出此时从磁场上边界垂直射出的粒子在磁场中运动的时间；
(4)当磁场中的磁感应强度大小为第(3)问中B0的
倍时，求能从磁场上边界射出粒子的边界宽度。
【答案】(1) 
；
(2) 
；
(3)
，
；
(4)
.
【解析】
⑴设粒子被电场加速后速度为v，由动能定理得：
①
粒子经电场加速后在圆形区域内运动的时间：
②
得：③
⑵粒子在磁场中做匀速圆周运动，设轨道半径为r0。从a点进入磁场的粒子不能从磁场上边界射出磁场应满足：
④
由
⑤
得：⑥
⑶垂直磁场上边界射出的粒子的圆心O必在磁场上边界上，设该粒子做匀速圆周运动的轨道半径为r，满足磁感应强度有最大值，即r有最小值。又因为
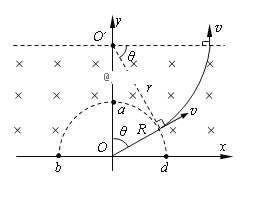
⑦
当r有最小值时，OO取最小值，OO最小值为O点到磁场上边界的距离2R
故：
⑧
由以上各式可得：⑨
设此时粒子进入磁场时速度方向与y轴正方向的夹角为θ
则
故
由于带电粒子在磁场中的运动周期：
⑩
此时垂直于磁场上边界射出磁场的粒子在磁场中运动的时间：
⑷当B=
时，带电粒子在磁场中的运动半径
由几何知识可知，当粒子从d点沿x轴正方向进入磁场，粒子从磁场上边界射出点，为粒子能够到达的上边界的最右端。设粒子能够到达的上边界的最右端距y轴的距离为x1
得：
当粒子与磁场上边界相切时，切点为粒子能够到达的上边界的最左端。设粒子能够到达的上边界的最左端距y轴的距离为x2
得：
粒子能从磁场上边界射出粒子的边界宽度：
