题目内容
2. 一水平抛出的小球落到一倾角为θ=30°的斜面上时,其速度方向与斜面垂直,运动轨迹如图中虚线所示.小球在竖直方向下落的距离与在水平方向通过的距离之比为( )
一水平抛出的小球落到一倾角为θ=30°的斜面上时,其速度方向与斜面垂直,运动轨迹如图中虚线所示.小球在竖直方向下落的距离与在水平方向通过的距离之比为( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 物体做平抛运动,我们可以把平抛运动可以分解为水平方向上的匀速直线运动,和竖直方向上的自由落体运动来求解,两个方向上运动的时间相同.根据平抛运动的规律分别求出速度与水平方向夹角的正切值和位移与水平方向夹角的正切值,从而得出小球在水平方向通过的距离与在竖直方向下落的距离之比.
解答 解:小球撞在斜面上,速度方向与斜面垂直,速度方向与水平方向夹角的正切值$tan60°=\frac{{v}_{y}}{{v}_{0}}=\sqrt{3}$=$\frac{gt}{{v}_{0}}$,
竖直位移与水平位移的比值$tanα=\frac{\frac{1}{2}g{t}^{2}}{{v}_{0}t}=\frac{gt}{2{v}_{0}}=\frac{1}{2}tan60°$=$\frac{\sqrt{3}}{2}$.
故选:D.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解.

练习册系列答案
相关题目
4. 如图所示,在B=0.1T的匀强磁场中有一边长为L=8cm的正方形ABCD,内有一点P,它与AD和DC的距离均为1cm,在P点有一个发射正离子的装置,能够连续不断地向纸面内的各个方向发射出速率不同的正离子,离子的质量为1.0×10-14kg,电荷量为1.0×10-5C,离子的重力不计,不考虑离子之间的相互作用,则( )
如图所示,在B=0.1T的匀强磁场中有一边长为L=8cm的正方形ABCD,内有一点P,它与AD和DC的距离均为1cm,在P点有一个发射正离子的装置,能够连续不断地向纸面内的各个方向发射出速率不同的正离子,离子的质量为1.0×10-14kg,电荷量为1.0×10-5C,离子的重力不计,不考虑离子之间的相互作用,则( )
 如图所示,在B=0.1T的匀强磁场中有一边长为L=8cm的正方形ABCD,内有一点P,它与AD和DC的距离均为1cm,在P点有一个发射正离子的装置,能够连续不断地向纸面内的各个方向发射出速率不同的正离子,离子的质量为1.0×10-14kg,电荷量为1.0×10-5C,离子的重力不计,不考虑离子之间的相互作用,则( )
如图所示,在B=0.1T的匀强磁场中有一边长为L=8cm的正方形ABCD,内有一点P,它与AD和DC的距离均为1cm,在P点有一个发射正离子的装置,能够连续不断地向纸面内的各个方向发射出速率不同的正离子,离子的质量为1.0×10-14kg,电荷量为1.0×10-5C,离子的重力不计,不考虑离子之间的相互作用,则( )| A. | 速率为5×106m/s的离子在磁场中运动的半径是5cm | |
| B. | 速率在5×105m/s到8×105m/s范围内的离子不可能射出正方形区域 | |
| C. | 速率为5×106m/s的离子在CB边上可以射出磁场的范围为距C点距离2cm~(1+$\sqrt{21}$)cm | |
| D. | 离子从CB边上射出正方形区域的最小速度为(8-$\sqrt{14}$)×106m/s |
13.甲乙两辆汽车在平直的公路上沿同一方向做匀变速直线运动,t=0时刻同时经过公路旁的同一路标,下表是每隔1s记录的两车的速率.关于两车的运动,下列说法正确的是( )
| 时间t/s | 0 | 1 | 2 | 3 | 4 |
| 甲车的速率v1/(m•s-1) | 18.0 | 16.0 | 14.0 | 12.0 | 10.0 |
| 乙车的速率v2/(m•s-1) | 3.0 | 4.0 | 5.0 | 6.0 | 7.0 |
| A. | 乙车的速度变化率较大 | |
| B. | 在0~4s内,乙车的平均速度较大 | |
| C. | 在0~4s内,甲车相对乙车行驶了56m | |
| D. | 在乙车追上甲车之前,t=5 s时两车相距最远 |
17. 如图所示,A、B两端滑块用轻绳连接,在拉力F作用下沿倾角为θ的斜面匀加速上滑,已知拉力F沿斜面向上,保证在各种情况下F的大小都不变且A、B都能沿斜面向上作匀加速运动,对于A、B间绳子的弹力,下列有关判断正确的是( )
如图所示,A、B两端滑块用轻绳连接,在拉力F作用下沿倾角为θ的斜面匀加速上滑,已知拉力F沿斜面向上,保证在各种情况下F的大小都不变且A、B都能沿斜面向上作匀加速运动,对于A、B间绳子的弹力,下列有关判断正确的是( )
 如图所示,A、B两端滑块用轻绳连接,在拉力F作用下沿倾角为θ的斜面匀加速上滑,已知拉力F沿斜面向上,保证在各种情况下F的大小都不变且A、B都能沿斜面向上作匀加速运动,对于A、B间绳子的弹力,下列有关判断正确的是( )
如图所示,A、B两端滑块用轻绳连接,在拉力F作用下沿倾角为θ的斜面匀加速上滑,已知拉力F沿斜面向上,保证在各种情况下F的大小都不变且A、B都能沿斜面向上作匀加速运动,对于A、B间绳子的弹力,下列有关判断正确的是( )| A. | 斜面倾角θ越大,绳子的弹力也越大 | |
| B. | 斜面的粗糙程度越大,绳子的弹力也越大 | |
| C. | 倾角θ越小,斜面越光滑,绳子弹力也越小 | |
| D. | 绳子弹力大小与斜面粗糙程度和倾角大小无关 |
7.如图是某质点运动的速度图象,由图象得到的正确结果是( )


| A. | 0~1s内的平均速度是2m/s | |
| B. | 0~1s内的加速度等于2~4s内的加速度 | |
| C. | 0~1s内的平均速度等于2~4s内的平均速度 | |
| D. | 0~1s内的运动方向与2~4s内的运动方向相反 |
14. 如图所示,固定的光滑绝缘斜面的底端固定着一个带正电的小物块P,将另一个带电小物块Q在斜面的某位置由静止释放,它将沿斜面向上运动.设斜面足够长,则在Q向上运动过程中( )
如图所示,固定的光滑绝缘斜面的底端固定着一个带正电的小物块P,将另一个带电小物块Q在斜面的某位置由静止释放,它将沿斜面向上运动.设斜面足够长,则在Q向上运动过程中( )
 如图所示,固定的光滑绝缘斜面的底端固定着一个带正电的小物块P,将另一个带电小物块Q在斜面的某位置由静止释放,它将沿斜面向上运动.设斜面足够长,则在Q向上运动过程中( )
如图所示,固定的光滑绝缘斜面的底端固定着一个带正电的小物块P,将另一个带电小物块Q在斜面的某位置由静止释放,它将沿斜面向上运动.设斜面足够长,则在Q向上运动过程中( )| A. | 物块P、Q的电势能和动能之和先增大后减小 | |
| B. | 物块P、Q的重力势能和电势能之和先减小后增大 | |
| C. | 物块P、Q的重力势能和电势能之和先增大后减小 | |
| D. | 物块P、Q的重力势能和动能之和先增大后减小 |
11.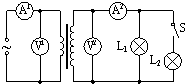 为探究理想变压器原、副线圈电压、电流的关系,将原线圈接到电压有效值不变的正弦交流电源上,副线圈连接相同的灯泡L1、L2,电路中分别接了理想交流电压表V1、V2和理想交流电流表A1、A2,导线电阻不计,如图所示.当开关S闭合后( )
为探究理想变压器原、副线圈电压、电流的关系,将原线圈接到电压有效值不变的正弦交流电源上,副线圈连接相同的灯泡L1、L2,电路中分别接了理想交流电压表V1、V2和理想交流电流表A1、A2,导线电阻不计,如图所示.当开关S闭合后( )
 为探究理想变压器原、副线圈电压、电流的关系,将原线圈接到电压有效值不变的正弦交流电源上,副线圈连接相同的灯泡L1、L2,电路中分别接了理想交流电压表V1、V2和理想交流电流表A1、A2,导线电阻不计,如图所示.当开关S闭合后( )
为探究理想变压器原、副线圈电压、电流的关系,将原线圈接到电压有效值不变的正弦交流电源上,副线圈连接相同的灯泡L1、L2,电路中分别接了理想交流电压表V1、V2和理想交流电流表A1、A2,导线电阻不计,如图所示.当开关S闭合后( )| A. | A1示数不变,A1与A2示数的比值不变 | |
| B. | A1示数变大,A1与A2示数的比值变大 | |
| C. | V2示数变小,V1与V2示数的比值变大 | |
| D. | V2示数不变,V1与V2示数的比值不变 |
12.如图所示,真空中相距d=10cm的两块平行金属板A、B与电源连接(图中未画出),其中B板接地(电势为零),A板电势变化的规律如图所示其中T=1.0×10-5s.将一个质量m=2.0×10-23kg,电量q=+1.6×10-15C的带电粒子从紧邻B板处由静止释放,不计带电粒子重力且粒子接触AB极板就会被吸收,下列说法正确的是( )


| A. | 若在t=0时刻释放该带电粒子,则该粒子将在AB极板之间做往返运动 | |
| B. | 若在t=$\frac{T}{4}$时刻释放该粒子,则该粒子能打中A极板 | |
| C. | 若在0~$\frac{T}{4}$之间某时刻释放该带电粒子,则该粒子一定能打到A极板 | |
| D. | 若在$\frac{T}{4}$~$\frac{T}{2}$之间某时刻释放带电粒子,则该粒子在AB极板之间往返运动 |