题目内容
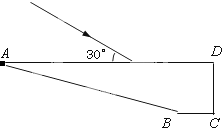
如图所示,ABCD是由某玻璃制成的梯形柱体横截面,AD面为水平面,∠A=15°,∠C=∠D=90°,今有一束激光以与AD成30°的夹角射向柱体的AD平面,玻璃对此光的折射率为
,部分光经AD面折射后射到AB面上的P点(图中未画出).若P点到AD面的距离为1.5
cm,P点到CD面的距离为3cm,求:出射点到AD的距离.
| 3 |
| 3 |

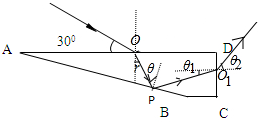
光路如图所示,入射的激光到达AD界面后,一部分发生反射,一部分折射到达AB面,设折射角为r.
由折射定律得:n=
,解得:r=30°
设临界角为C,由折射定律得:sinC=
,故C=arcsin
<45°.
由几何关系知,射向AB面的光入射角为 θ=45°>C,故将光线在AB面上发生全反射,并到达CD界面,
如图,由几何知识得:θ1=30°
由
=n得,sinθ2=nsinθ1=
sin30°=
解得:θ2=60°
由几何关系得:O1D=(1.5
-3tan30°)cm=0.5
cm
答:出射点到AD的距离是0.5
cm.
由折射定律得:n=
| sin60° |
| sinr |
设临界角为C,由折射定律得:sinC=
| 1 |
| n |
| ||
| 3 |
由几何关系知,射向AB面的光入射角为 θ=45°>C,故将光线在AB面上发生全反射,并到达CD界面,
如图,由几何知识得:θ1=30°
由
| sinθ2 |
| sinθ1 |
| 3 |
| ||
| 2 |
解得:θ2=60°
由几何关系得:O1D=(1.5
| 3 |
| 3 |
答:出射点到AD的距离是0.5
| 3 |


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目