题目内容
如图所示,AOB是由某种透明物质制成的
圆柱体横截面(O为圆心)折射率为
.今有一束平行光以45°的入射角射向柱体的OA平面,这些光线中有一部分不能从柱体的AB面上射出,设凡射到OB面的光线全部被吸收,也不考虑OA面的反射,求圆柱AB面上能射出光线的部分占AB表面的几分之几?

| 1 |
| 4 |
| 2 |

从O点射入的光线,折射角为r,根据折射定律有:n=
①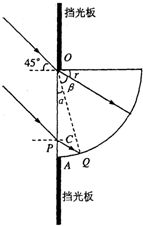
解得 r=30°②
从某位置P点入射的光线,折射到AB弧面上Q点时,入射角恰等于临界角C,有:sinC=
③
代入数据得:C=45°④
△PQO中∠α=180°-90°-r=15°
所以能射出的光线区域对应的圆心角β=90°-α-r=45°⑥
能射出光线的部分占AB面的比例为
=
⑦
答:圆柱AB面上能射出光线的部分占AB表面的
.
| sin45° |
| sinr |

解得 r=30°②
从某位置P点入射的光线,折射到AB弧面上Q点时,入射角恰等于临界角C,有:sinC=
| 1 |
| n |
代入数据得:C=45°④
△PQO中∠α=180°-90°-r=15°
所以能射出的光线区域对应的圆心角β=90°-α-r=45°⑥
能射出光线的部分占AB面的比例为
| 45° |
| 90° |
| 1 |
| 2 |
答:圆柱AB面上能射出光线的部分占AB表面的
| 1 |
| 2 |

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目