题目内容
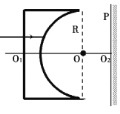
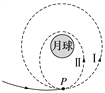
【题目】一足够长的水平绝缘轨道上有A、B两物体处于静止状态,在AB之间的空间存在水平向右的匀强电场,场强为E。A物体带正电,电量为q,小物块B不带电且绝缘,如图所示。小物体A由静止释放,一段时间后与B发生弹性碰撞(碰撞时间极短);当A返回到轨道上的P点(图中未标出)时,速度减为0,再过一段时间A刚好能到达B再次静止的位置。A物体在电场中第一次加速所用时间等于A在电场中向左减速所用时间的2.5倍。物体A与轨道的动摩擦因数为μ1,B与轨道的动摩擦因数为μ2,其中的μ1和μ2均为未知量。已知A的质量为m,B的质量为3m。初始时A与B的距离为d,重力加速度大小为g,不计空气阻力。整个运动过程中,求物块A克服摩擦力所做的功。

【答案】![]()
【解析】
设A向右加速到B处时速度为v所用时间为t,A与B发生弹性碰撞 则:
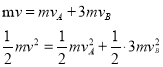
解得:
![]()
![]()
对A第一次向右加速,向左减速运动过程:

对A 在第一次向右加速过程中 由动能定理:
![]()
对A 在反弹后向左减速过程中 由动能定理:
![]()
全过程能量守恒:
![]()
联立整理可以得到:
![]()

练习册系列答案
相关题目