题目内容
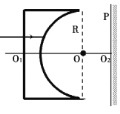
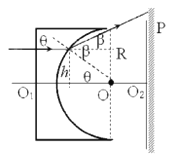
【题目】如图所示，从长方体透明玻璃中挖去一个半径为R的半球体，O为半球的球心，O1O2连线为透明玻璃体的主光轴，在离球心0.5R处竖直放置一个足够大的光屏，O2为屏上的点，让一单色光束平行O1O2垂直左侧表面入射，当光线距离O1O2连线0.5R时，折射后的光线达到光屏上距离O2为
R的P点，已知透明体的上下侧面均涂有吸光材料，则：
①透明玻璃的折射率为多少；
②当平行光线到光轴O1O2的距离为多少时，折射后射到光屏上的位置离O2最远。
【答案】①
；②
【解析】
①依题意可知，光线距离
连线0.5R平行入射时，入射角为
，折射角为
，设PO与夹角为
，则有
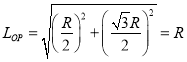
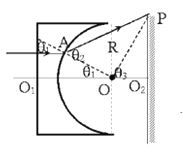
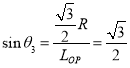
则有
所以
由折射定律可知
代入数据得
②当光线紧贴右侧上边缘射出时，达到光屏上的位置最远，设此时光线离光轴的距离为h，入射角为
，折射角为
，则有
由集合关系可知：
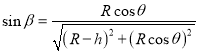
由折射定律可知
代入数据得
练习册系列答案
名校课堂系列答案
相关题目
