题目内容
9.在一足够长的倾角为θ=37°的光滑斜面顶端,由静止释放小球A,经过时间t=1s后,仍在斜面顶端水平抛出另一小球B,为使抛出的小球B刚好能够击中小球A,小球B应以多大速度抛出?(已知重力加速度为g=10m/s2,sin37°=0.6,cos37°=0.8)分析 平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,抓住两球的运动时间相等,水平位移相等,通过运动学公式求出小球B的速度.
解答 解:设B球平抛后经时间t1落到斜面上
其水平位移x=vt1…①
竖直位移$y=\frac{1}{2}{gt}_{1}^{2}$…②
考虑到斜面倾角有:y=xtanθ…③
根据①②③得,${t}_{1}=\frac{2vtan37°}{g}$…④
B球的位移为s=$\frac{x}{cosθ}=\frac{v{t}_{1}}{cosθ}=\frac{15{v}^{2}}{8g}$…⑤
而在这段时间内A球的总位移l=$\frac{1}{2}gsinθ({t}_{1}+1)^{2}$…⑥
因为两球相碰,则s=l…⑦
由⑤⑥⑦得,v=gt=10m/s
答:小球B应以10m/s的速度抛出
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,运用运动学公式灵活求解

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
20.关于电功、电功率,下列说法中正确的是( )
| A. | 电功的实质就是电场力所做的功 | |
| B. | 电功是其他形式能量转化为电能的量度 | |
| C. | 电功率是表示电流单位时间内产生的热量 | |
| D. | 一段电路上电功的大小等于两端电压、电路中电流和时间三者的乘积 |
17.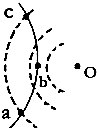 一带电粒子射入一固定在O点的点电荷的电场中,粒子运动轨迹如图中实线abc所示.图中虚线是同心圆弧,表示电场的等势面.不计重力,可以判断( )
一带电粒子射入一固定在O点的点电荷的电场中,粒子运动轨迹如图中实线abc所示.图中虚线是同心圆弧,表示电场的等势面.不计重力,可以判断( )
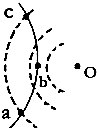 一带电粒子射入一固定在O点的点电荷的电场中,粒子运动轨迹如图中实线abc所示.图中虚线是同心圆弧,表示电场的等势面.不计重力,可以判断( )
一带电粒子射入一固定在O点的点电荷的电场中,粒子运动轨迹如图中实线abc所示.图中虚线是同心圆弧,表示电场的等势面.不计重力,可以判断( )| A. | 此粒子一直受到静电吸引力作用 | |
| B. | 粒子在b点的电势能一定大于在a点的电势能 | |
| C. | 粒子在a 点和c点的速度相同 | |
| D. | 粒子在b 点的速度一定大于在a 点的速度 |
4.如图甲所示,面积为0.1m2的10匝线圈EFG处在某磁场中,t=0时,磁场方向垂直于线圈平面向里,磁感应强度B随时间变化的规律如图乙所示.已知线圈与右侧电路接触良好,电路中的电阻R=4Ω,电容C=10 μF,线圈EFG的电阻为1Ω,其余部分电阻不计.则当开关S闭合,电路稳定后,在t=0.1s至t=0.2s这段时间内( )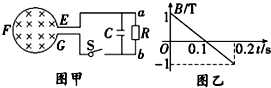

| A. | 电容器所带的电荷量为8×10-5 C | B. | 通过R的电流是2.5 A,方向从b到a | ||
| C. | 通过R的电流是2 A,方向从b到a | D. | R消耗的电功率是0.16 W |
14.关于斜抛运动的性质以下说法正确的是( )
| A. | 斜抛运动是匀变速运动,因为其速度是恒定的 | |
| B. | 斜抛运动是匀变速运动,因为其加速度是恒定的 | |
| C. | 斜抛运动是非匀变速运动,因为其速度是变化的 | |
| D. | 斜抛运动是非匀变速运动,因为其加速度是变化的 |
18.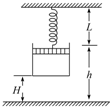 如图所示,一导热性良好的汽缸内用活塞封住一定量的气体(不计活塞与缸壁摩擦),当温度升高时,改变的量有( )
如图所示,一导热性良好的汽缸内用活塞封住一定量的气体(不计活塞与缸壁摩擦),当温度升高时,改变的量有( )
 如图所示,一导热性良好的汽缸内用活塞封住一定量的气体(不计活塞与缸壁摩擦),当温度升高时,改变的量有( )
如图所示,一导热性良好的汽缸内用活塞封住一定量的气体(不计活塞与缸壁摩擦),当温度升高时,改变的量有( )| A. | 活塞高度h | B. | 汽缸底距地面高度H | ||
| C. | 气体压强p | D. | 弹簧长度L |
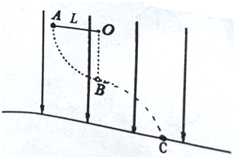 空间有E=100V/m竖直向下的匀强电场,长L=0.8m不可伸长的轻绳固定于O点,另一端系一质量m=0.1kg,电量q=0.01C的带正电小球.拉起绝缘小球至绳水平的A点,然后无初速度释放小球,当小球运动至O点的正下方B点时绳恰好断裂,小球继续运动,最后落至地面上C点,B点离地的高度hB=0.2m.(g取10m/s2)试求:
空间有E=100V/m竖直向下的匀强电场,长L=0.8m不可伸长的轻绳固定于O点,另一端系一质量m=0.1kg,电量q=0.01C的带正电小球.拉起绝缘小球至绳水平的A点,然后无初速度释放小球,当小球运动至O点的正下方B点时绳恰好断裂,小球继续运动,最后落至地面上C点,B点离地的高度hB=0.2m.(g取10m/s2)试求: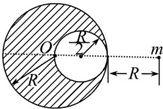 如图所示,在距一质量为m0、半径为R、密度均匀的大球体R处有一质量为m的质点,此时大球体对质点的万有引力为F1,当从大球体中挖去一半径为$\frac{R}{2}$的小球体后(空腔的表面与大球体表面相切),剩下部分对质点的万有引力为F2,求F1:F2.
如图所示,在距一质量为m0、半径为R、密度均匀的大球体R处有一质量为m的质点,此时大球体对质点的万有引力为F1,当从大球体中挖去一半径为$\frac{R}{2}$的小球体后(空腔的表面与大球体表面相切),剩下部分对质点的万有引力为F2,求F1:F2.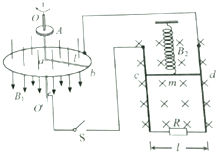 为了探究电动机转速与弹簧伸长量之间的关系,小明设计了如图所示的装置.半径为l的圆形金属导轨固定在水平面上,一根长也为l、电阻为R的金属棒ab一端与导轨接触良好,另一端固定在圆心处的导电转轴oo’上,由电动机A带动旋转.在金属导轨区域内存在垂直于导轨平面,大小为B1、方向竖直向下的匀强磁场.另有一质量为m、电阻为R的金属棒cd用轻质弹簧悬挂在竖直平面内,并与固定在竖直平面内的“U”型导轨保持良好接触,导轨间距为l,底部接阻值也为R的电阻,处于大小为B2、方向垂直导轨平面向里的匀强磁场中,从圆形金属导轨引出导线和通过电刷从转轴引出导线经开关S与“U”型导轨连接.当开关S断开,棒cd静止时,弹簧伸长量为x0;当开关S闭合,电动机以某一速度匀速转动,棒cd再次静止,弹簧伸长量变为x(不超过弹性限度).不计其余电阻和摩擦等阻力,求此时
为了探究电动机转速与弹簧伸长量之间的关系,小明设计了如图所示的装置.半径为l的圆形金属导轨固定在水平面上,一根长也为l、电阻为R的金属棒ab一端与导轨接触良好,另一端固定在圆心处的导电转轴oo’上,由电动机A带动旋转.在金属导轨区域内存在垂直于导轨平面,大小为B1、方向竖直向下的匀强磁场.另有一质量为m、电阻为R的金属棒cd用轻质弹簧悬挂在竖直平面内,并与固定在竖直平面内的“U”型导轨保持良好接触,导轨间距为l,底部接阻值也为R的电阻,处于大小为B2、方向垂直导轨平面向里的匀强磁场中,从圆形金属导轨引出导线和通过电刷从转轴引出导线经开关S与“U”型导轨连接.当开关S断开,棒cd静止时,弹簧伸长量为x0;当开关S闭合,电动机以某一速度匀速转动,棒cd再次静止,弹簧伸长量变为x(不超过弹性限度).不计其余电阻和摩擦等阻力,求此时