题目内容
7. 用一根细绳,一端系住一定质量的小球,另一端固定,使小球在水平面内做匀速圆周运动.现有两个这样的装置,如图甲和乙所示.已知两球转动的角速度大小相同,绳与竖直方向的夹角分别为37°和53°.则a、b两球的转动半径Ra和Rb之比为9:16.绳子受到的拉力之比为3:4 (sin 37°=0.6;cos 37°=0.8)
用一根细绳,一端系住一定质量的小球,另一端固定,使小球在水平面内做匀速圆周运动.现有两个这样的装置,如图甲和乙所示.已知两球转动的角速度大小相同,绳与竖直方向的夹角分别为37°和53°.则a、b两球的转动半径Ra和Rb之比为9:16.绳子受到的拉力之比为3:4 (sin 37°=0.6;cos 37°=0.8)
分析 小球做圆周运动的向心力由绳子的拉力和重力的合力提供,根据牛顿第二定律求出角速度与半径的关系,从而得出转动半径之比,根据几何关系求出绳子拉力与重力的关系,从而求出拉力之比.
解答 解:小球所受的合力为:F合=mgtanθ=mRω2,解得:R=$\frac{gtanθ}{{ω}^{2}}$,由于角速度大小相等,则转动的半径比为:Ra:Rb=tan37°:tan53°=9:16,
根据几何关系得:
绳子的拉力T=$\frac{mg}{cosθ}$,
绳子受到的拉力之比为Ta:Tb=cos53°:cos37°=3:4.
故答案为:9:16;3:4
点评 解决本题的关键知道小球圆周运动的向心力的来源,根据牛顿第二定律进行求解,本题中角速度相等,所以列式时要列角速度的表达式,难度不大,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18. 在如图所示的空间中,存在电场强度为E的匀强电场,同时存在沿x轴负方向、磁感应强度大小为B的匀强磁场.一质子(电荷量为e,不计重力)在该空间恰沿y轴正方向以速度v匀速运动,据此可以判断出( )
在如图所示的空间中,存在电场强度为E的匀强电场,同时存在沿x轴负方向、磁感应强度大小为B的匀强磁场.一质子(电荷量为e,不计重力)在该空间恰沿y轴正方向以速度v匀速运动,据此可以判断出( )
 在如图所示的空间中,存在电场强度为E的匀强电场,同时存在沿x轴负方向、磁感应强度大小为B的匀强磁场.一质子(电荷量为e,不计重力)在该空间恰沿y轴正方向以速度v匀速运动,据此可以判断出( )
在如图所示的空间中,存在电场强度为E的匀强电场,同时存在沿x轴负方向、磁感应强度大小为B的匀强磁场.一质子(电荷量为e,不计重力)在该空间恰沿y轴正方向以速度v匀速运动,据此可以判断出( )| A. | 质子所受电场力大小等于eE,运动中电势能减小;沿z轴正方向电势升高 | |
| B. | 质子所受电场力大小等于eE,运动中电势能增大;沿z轴正方向电势降低 | |
| C. | 质子所受电场力大小等于evB,运动中电势能不变;沿z轴正方向电势降低 | |
| D. | 质子所受电场力大小等于evB,运动中电势能不变;沿z轴正方向电势升高 |
2. 如图所示,在竖直平面内的正方形ABCD区域内有平行于AB边的匀强电场,E、F、G、H是各边中点,其连线构成正方形,其中P点是EH的中点.一个带负电的粒子(不计重力)以初动能Ek从F点沿FH方向射入电场后恰好从D点射出.以下说法正确的是( )
如图所示,在竖直平面内的正方形ABCD区域内有平行于AB边的匀强电场,E、F、G、H是各边中点,其连线构成正方形,其中P点是EH的中点.一个带负电的粒子(不计重力)以初动能Ek从F点沿FH方向射入电场后恰好从D点射出.以下说法正确的是( )
 如图所示,在竖直平面内的正方形ABCD区域内有平行于AB边的匀强电场,E、F、G、H是各边中点,其连线构成正方形,其中P点是EH的中点.一个带负电的粒子(不计重力)以初动能Ek从F点沿FH方向射入电场后恰好从D点射出.以下说法正确的是( )
如图所示,在竖直平面内的正方形ABCD区域内有平行于AB边的匀强电场,E、F、G、H是各边中点,其连线构成正方形,其中P点是EH的中点.一个带负电的粒子(不计重力)以初动能Ek从F点沿FH方向射入电场后恰好从D点射出.以下说法正确的是( )| A. | 粒子的运动轨迹一定经过PH之间某点 | |
| B. | 粒子在D点的电势能比在F点少了Ek | |
| C. | 若将粒子的初速度变为原来的一半,粒子由E点射出电场 | |
| D. | 若加一垂直ABCD区域向外的匀强磁场,粒子可能会从H点射出电场 |
12. 如图所示,abcd为一边长为L、匝数为N的正方形闭合线圈,绕对称轴OO′匀速转动,角速度为ω.空间中只有OO′左侧存在垂直纸面向里的匀强磁场,磁感应强度为B.若闭合线圈的总电阻为R,则( )
如图所示,abcd为一边长为L、匝数为N的正方形闭合线圈,绕对称轴OO′匀速转动,角速度为ω.空间中只有OO′左侧存在垂直纸面向里的匀强磁场,磁感应强度为B.若闭合线圈的总电阻为R,则( )
 如图所示,abcd为一边长为L、匝数为N的正方形闭合线圈,绕对称轴OO′匀速转动,角速度为ω.空间中只有OO′左侧存在垂直纸面向里的匀强磁场,磁感应强度为B.若闭合线圈的总电阻为R,则( )
如图所示,abcd为一边长为L、匝数为N的正方形闭合线圈,绕对称轴OO′匀速转动,角速度为ω.空间中只有OO′左侧存在垂直纸面向里的匀强磁场,磁感应强度为B.若闭合线圈的总电阻为R,则( )| A. | 当线圈转到图示位置时,穿过线圈的磁通量变化率最大 | |
| B. | 线圈中电动势的有效值为$\frac{\sqrt{2}}{4}$NBL2ω | |
| C. | 线圈转一圈外力至少做功为$\frac{π}{2R}$N2B2L4ω | |
| D. | 当线圈从图示位置转动半圈的过程中,通过线圈横截面的电量为$\frac{NB{L}^{2}}{2R}$ |
19.在物理学发展过程中,科学的物理思想方法对物理学的发展起到了重要作用,下列关于物理思想方法说法不正确的是( )
| A. | 质点和点电荷是同一种思想方法 | |
| B. | 合力和分力、总电阻都体现了等效替代的思想 | |
| C. | 伽利略用小球在斜面上的运动验证了速度与位移成正比 | |
| D. | 加速度、电场强度、电势都是采取比值法定义的物理量 |
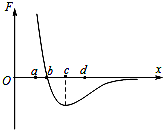 如图所示,甲分子固定在坐标原点O,乙分子位于x轴上,甲分子对乙分子的作用力与两分子间距离的关系如图中曲线所示,F>0为斥力,F<0为引力,a、b、c、d为x轴上四个特定的位置,则在这四个点中,该系统分子势能最低的位置在点( )
如图所示,甲分子固定在坐标原点O,乙分子位于x轴上,甲分子对乙分子的作用力与两分子间距离的关系如图中曲线所示,F>0为斥力,F<0为引力,a、b、c、d为x轴上四个特定的位置,则在这四个点中,该系统分子势能最低的位置在点( )
 如下图,水平转盘上放有质量为m的物体(可视为质点),连接物体和转轴的绳子的长为r,物块与转盘间的最大静摩擦力是其压力的μ倍,转盘的角速度由零逐渐增大,试通过计算求:
如下图,水平转盘上放有质量为m的物体(可视为质点),连接物体和转轴的绳子的长为r,物块与转盘间的最大静摩擦力是其压力的μ倍,转盘的角速度由零逐渐增大,试通过计算求:
