Question

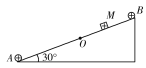
【题目】如图所示，倾角为30°的粗糙绝缘斜面固定在水平面上，在斜面的底端A和顶端B分别固定等量的同种正电荷。质量为m、带电荷量为＋q的物块从斜面上的M点由静止释放，物块向下运动的过程中经过斜面中点O时速度达到最大值v，运动的最低点为N(图中没有标出)，则下列说法正确的是

A. 物块向下运动的过程中加速度先增大后减小

B. 物块和斜面间的动摩擦因数μ=

C. 物块运动的最低点N到O点的距离小于M点到O点的距离

D. 物块的释放点M与O点间的电势差为

Answer 1

【答案】D

【解析】

根据点电荷的电场特点和电场的叠加原理可知，沿斜面从A到B电场强度先减小后增大，中点O的电场强度为零。设物块下滑过程中的加速度为a，根据牛顿第二定律有mgsin θ－μmgcos θ＋qE=ma，物块下滑的过程中电场力qE先方向沿斜面向下逐渐减少后沿斜面向上逐渐增加，所以物块的加速度大小先减小后增大，选项A错误；物块在斜面上运动到O点时的速度最大，加速度为零，又电场强度为零，所以有mgsinθ－μmgcosθ=0，所以物块和斜面间的动摩擦因数μ=tanθ=，选项B错误；由于运动过程中mgsinθ－μmgcosθ=0，所以物块从M点运动到N点的过程中受到的合外力为qE，因此最低点N与释放点M关于O点对称，选项C错误；根据动能定理有qUMO＋mgxMOsinθ－μmgxMOcosθ=mv2，且mgsinθ=μmgcosθ，所以物块的释放点M与O点间的电势差UMO=，选项D正确。