Question

【题目】如图所示，在直角坐标系xoy的第一象限中有两个全等的直角三角形区域Ⅰ和Ⅱ，充满了方向均垂直纸面向里的匀强磁场，区域Ⅰ的磁感应强度大小为B0，区域Ⅱ的磁感应强度大小可调， C点坐标为（4L，3L），M点为OC的中点。质量为m带电量为-q的粒子从C点以平行于y轴方向射入磁场Ⅱ中，速度大小为，不计粒子所受重力，粒子运动轨迹与磁场区域相切时认为粒子能再次进入磁场。

（1）若粒子无法进入区域Ⅰ中，求区域Ⅱ磁感应强度大小范围；

（2）若粒子恰好不能从AC边射出，求区域Ⅱ磁感应强度大小；

（3）若粒子能到达M点，求区域Ⅱ磁场的磁感应强度大小的所有可能值。

Answer 1

【答案】（1）；（2）；（3）若粒子由区域Ⅰ达到M点，n=1时， ；n=2时， ；n=3时， ；②若粒子由区域Ⅱ达到M点，n=0时， ，n=1时，

【解析】（1）粒子速度越大，半径越大，当运动轨迹恰好与x轴相切时，恰好不能进入Ⅰ区域

故粒子运动半径

粒子运动半径满足： 代入

解得

（2）粒子在区域Ⅰ中的运动半径

若粒子在区域Ⅱ中的运动半径R较小，则粒子会从AC边射出磁场。恰好不从AC边射出时满足∠O2O1Q=2θ

又

解得

代入

可得：

（3）①若粒子由区域Ⅰ达到M点

每次前进

由周期性： 即

，解得

n=1时，

n=2时，

n=3时，

②若粒子由区域Ⅱ达到M点

由周期性：

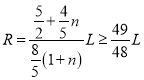即，解得，解得

n=0时，

n=1时，