��Ŀ����
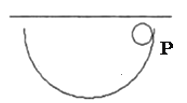
����Ŀ����ͼ��ʾ��һ����Ϊm���뾶Ϊr�Ĺ⻬��A��ϸ��������O�㣬��һ����ΪM���뾶ΪR�İ���������B��������ֱǽ�ں�A��֮�䣬B�����ĵ�O��֮��ľ���Ϊh��A��B��������ͬһˮƽ���ϣ�A��B���ھ�ֹ״̬���������ٶ�Ϊg��������˵����ȷ����

A. A��B��ѹ����СΪ![]()
B. ��ֱǽ�ڶ�B��Ħ��������Ϊ��
C. ��ֻ�������B�����ƶ�һ����룬��A��B�ٴα��־�ֹ����A��B��ѹ����С���ֲ��䣬ϸ����������
D. ��ֻ�������B�����ƶ�һ����룬��A��B�ٴα��־�ֹ����A��B��ѹ����С��ϸ��������С
���𰸡�AD
��������
����С���������������úϳɷ���ͼ������������������B��A��֧�������Ӷ����A��B��ѹ��.����B�������������ƽ�������ж�ǽ�ڶ�B��Ħ����.��ֻ�������B�����ƶ�һ����룬����ͬ���ķ����õ�B��A��֧������ϸ�������ı���ʽ�����ɷ������ǵı仯.
A������A��������������ͼ1��ʾ��
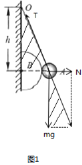
N��mg�ĺ�����T�ȴ����ߣ�����������Ӱ���������Ƶã�![]() ���ã�
���ã�![]() ��
��![]() ����ţ�ٵ�������֪A��B��ѹ����СΪ��
����ţ�ٵ�������֪A��B��ѹ����СΪ��![]() ����A��ȷ.
����A��ȷ.
B��B����ֱ�����ܵ���������AB����Ħ������ƽ������֪��ֱǽ�ڶ�Bһ����Ħ��������B����.
CD����ֻ�������B�����ƶ�һ����룬����A��������������ͼ2��ʾ��
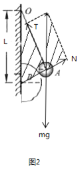
N��T�ĺ�����mg�ȴ����ߣ�����������Ӱ���������Ƶã�![]()
�ɵã�![]() ��
��![]() ������L��h����֪��N��С��T��С����ţ�ٵ�������֪A��B��ѹ����С����C����D��ȷ.
������L��h����֪��N��С��T��С����ţ�ٵ�������֪A��B��ѹ����С����C����D��ȷ.
��ѡAD.