题目内容
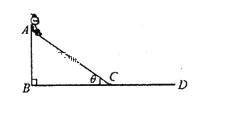
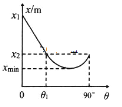
【题目】某物体以一定的初速度沿着斜面向上运动,它所能达到的最大位移x与斜面倾角![]() 的关系如图所示,已知x1、x2和重力加速度g,则可求出
的关系如图所示,已知x1、x2和重力加速度g,则可求出
A. 物体的初速度
B. 当物体位移为x2时对应的斜面倾角![]()
C. 物体在不同倾角的斜面上,减速到零时的位移最小值![]()
D. 当物体位移为最小值![]() 时,对应的滑动摩擦力大小
时,对应的滑动摩擦力大小
【答案】ABC
【解析】
由图象读出斜面倾角θ为90°时物体上升的高度,这种情况时,物块做竖直上抛运动,由由速度位移公式求出初速度;
由图象读出斜面倾角θ为0°时物体的位移,然后由速度位移公式求出加速度,再由牛顿第二定律求出动摩擦因数;
由牛顿第二定律和运动学公式结合得到x与θ的关系式,运用数学知识求解最小值及达到最小值的条件。
AB.由图知,当θ=90°时位移为![]() ,物体做竖直上抛运动,则有:
,物体做竖直上抛运动,则有:![]()
解得:![]() ,故A、B正确;
,故A、B正确;
CD.当θ为其他值时,对物块受力分析,物体的加速度大小为a,由牛顿第二定律得:
mgsin θ+μmgcos θ=ma
由运动学公式有:0-v02=-2ax
由以上各式得:![]()
由数学知识得:sin θ+μcos θ=![]() ,其中
,其中![]()
当θ=0°时位移为![]() 说明斜面粗糙,设物块与斜面间摩擦因数为μ,则物体的加速度大小为a0,则有:μmg=ma0
说明斜面粗糙,设物块与斜面间摩擦因数为μ,则物体的加速度大小为a0,则有:μmg=ma0
且有:![]()
可解得![]() ,综上所述可解得:物体在不同倾角的斜面上,减速到零时的位移最小值
,综上所述可解得:物体在不同倾角的斜面上,减速到零时的位移最小值![]()
由于不知道,物体的质量,所以无法确定摩擦力,故C正确,D错误。
故选:ABC。

练习册系列答案
相关题目