Question

如图，两根足够长的光滑固定平行金属导轨与水平面成θ角，导轨间距为d，两导体棒a和b与导轨垂直放置，两根导体棒的质量都为m、电阻都为R，回路中其余电阻不计．整个装置处于垂直于导轨平面向上的匀强磁场中，磁感应强度的大小为B，在t=0时刻使a沿导轨向上作速度为v的匀速运动，同时将b由静止释放，b经过一段时间后也作匀速运动．已知d=1m，m=0.5kg，R=0.5Ω，B=0.5T，θ=30⁰，g取10m/s²，不计两导棒间的相互作用力．
（1）若使导体棒b静止在导轨上，导体棒a向上运动的速度v多大？
（2）若a在平行于导轨向上的力F作用下，以v₁=2m/s的速度沿导轨向上匀速运动，试导出F与b的速率v₂的函数关系式并求出v₂的最大值；
（3）在（2）中，当t=2s时，b的速度达到5.06m/s，2s内回路中产生的焦耳热为13.2J，求该2s内力F做的功（结果保留三位有效数字）．

Answer 1

分析：（1）根据欧姆定律和安培力及受力平衡求出a的速度；
（2）对b受力分析找到力与速度的关系式，并根据极限情况求出v₂的最大值；
（3）根据第二问中的关系式进行微分求和代入数值即可解得内力F所做的功．

解答：解：（1）设a的速度为v₁，则电动势为：E=Bdv₁…①
电流为：I=

E

2R

…②
b受到的安培力为：F=BId…③
对b受力分析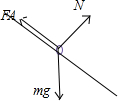如图，由平衡条件知：
F=mgsinθ…④
由①②③④式得：v₁=10m/s  
（2）设a的速度为v₁，b的速度为v₂，回路电流为I，
则：I=

E1+E2

2R

=

Bd(v1+v2)

2R

导体棒受到的安培力为：F′=B2d2(v1+v2)

1

2R

对a棒受力分析知：mgsinθ+B2d2(v1+v2)

1

2R

=F
代入数据得：F=3+

v2

4

（N）
设最大速度为v_m，对b棒受力分析知：

B2d2(v1+vm)

2R

=mgsinθ
数据得：v_m=8m/s 
（3）对b受力分析有：mgsinθ-F_A=ma  
解得：F_A=B2d2(v1+v2)

1

2R

即：mgsinθ-B2d2(v1+v2)

1

2R

=ma
用微元法计算b棒的位移，取任意无限小△t时间，b棒位移为v₂△t
对上式两边同乘以△t得：mgsinθ△t-B2d2(v1+v2)

1

2R

△t=ma△t 
代入数据并求和得：8t-x₂=2v₂ 
将t=2s，v₂=5.06m/s代入上式得：x₂=5.88m  
a的位移为：：x₁=v₁t=2×2=4m
由功能关系知：W_F=

1

2

mv

2 2

+mgx₁sinθ-mgx₂sinθ+Q
代入数据得：W_F=14.9J   
答：（1）若使导体棒b静止在导轨上，导体棒a向上运动的速度为10m/s．
（2）a在平行于导轨向上的力F作用下，以v₁=2m/s的速度沿导轨向上匀速运动，F=3+

v2

4

（N），最大速度为8m/s．
（3）在（2）中，当t=2s时，b的速度达到5.06m/s，2s内回路中产生的焦耳热为13.2J，求该2s内力F做的功为14.9J．

点评：此题考查的知识点比较多，对学生的数学知识的应用也要求比较高，是一道综合性较强的题目．