Question

【题目】如图，在光滑平直的轨道上有一节质量为M的车厢，车厢以12m/s的速度向右匀速运动，车厢顶部右侧边缘有一小物块（质量可忽略）与之相对静止．前方停着一质量m=3M的平板车，车顶离平板车高为h=1.8m．某时刻车厢与平板车相撞，车厢顶部的小物块顺势向前滑出．试问小物块将落在平板车上距离平板车左端多远的范围内？（不计空气阻力，平板车足够长，g=10m/s2）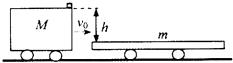

Answer 1

【答案】解：若车厢与平板车相碰后粘在一起共同运动，以向右为正，根据动量守恒定律得：Mv0=（M+m）v
代入数据解得：v=3m/s
小物块下落的时间为：t= ，
小物块相对于车的水平位移为：s1=（v0﹣v）t=5.4m，
若车厢与平板车相碰的过程中，没有能量损失，以向右为正，根据动量守恒定律和能量守恒定律得：
Mv0=Mv1+mv2 ，
，
解得： ，
则物块相对于车的水平位移为：s2=（v0﹣v2）t=3.6m，
所以小物块将落在平板车上距离平板车左端3.6m﹣5.4m的范围内．
答：小物块将落在平板车上距离平板车左端3.6m﹣5.4m的范围内
【解析】车厢和平板车组成的系统在碰撞前后瞬间动量守恒，分完全弹性碰撞和完全非弹性碰撞两种情况，根据动量守恒定律列式和能量守恒定律列式，小物体离开车厢做平抛运动，结合高度求出运动的时间，根据车厢碰撞前后瞬间的速度以及物块运动的时间求出小球相对于车的水平位移即可．
【考点精析】通过灵活运用平抛运动和动量守恒定律，掌握特点:①具有水平方向的初速度;②只受重力作用，是加速度为重力加速度g的匀变速曲线运动；运动规律:平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动；动量守恒定律成立的条件：系统不受外力或系统所受外力的合力为零；系统所受的外力的合力虽不为零，但系统外力比内力小得多；系统所受外力的合力虽不为零，但在某个方向上的分量为零，则在该方向上系统的总动量的分量保持不变即可以解答此题．