题目内容
【题目】一物体静止在光滑的水平面上,现对物体施加一个向右的水平恒力,使其产生向右的恒定加速度大小为a1 , 经过时间t速度为v1;此时撤去向右的恒力,并立即对它施加一个水平向左的恒力,使其产生向左的恒定加速度大小为a2 , 又经过时间t后物体回到出发点,速度大小为v2 . 求:
(1)两个物体的加速度大小的比值a1:a2
(2)两个物体的速度大小的比值v1:v2 .
【答案】
(1)解:经同样时间后回到原处,整个时间内物体的位移为零,
有: ![]() =0,
=0,
又v1=a1t,
解得a2=3a1,即a1:a2=1:3,
答:两个物体的加速度大小的比值为1:3.
(2)解:因为v2=v1﹣a2t=﹣2a1t=﹣2v1.
则速度大小之比v1:v2=1:2.
答:两个物体的速度大小的比值为1:2.
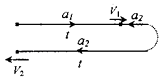
【解析】物体先做匀加速运动,后做匀减速运动回到原处,整个过程中的位移为零.结合位移时间公式得出加速度的关系,再结合速度时间公式得出速度的关系.
【考点精析】本题主要考查了匀变速直线运动的速度、位移、时间的关系和匀变速运动中的平均速度的相关知识点,需要掌握速度公式:V=V0+at;位移公式:s=v0t+1/2at2;速度位移公式:vt2-v02=2as;以上各式均为矢量式,应用时应规定正方向,然后把矢量化为代数量求解,通常选初速度方向为正方向,凡是跟正方向一致的取“+”值,跟正方向相反的取“-”值;平均速度:V=V0+Vt才能正确解答此题.

练习册系列答案
相关题目