题目内容
7.质量m=2000kg的汽车在水平路面上以v=36km/h的速度转弯,路面能提供的最大静摩擦力为车重的0.5倍.求:(1)当转弯半径r=40m时,其所需的向心力多大?
(2)为保证汽车不发生侧滑,转弯半径至少多大?(g取10m/s2)
分析 (1)根据向心力公式Fn=m$\frac{{v}^{2}}{r}$求汽车所需的向心力.
(2)汽车在水平路面上转弯时做圆周运动,汽车转弯时受重力、支持力和摩擦力作用,因为是水平面,所以汽车做圆周运动的向心力由路面给汽车的摩擦力提供.当静摩擦力达到最大时,转弯半径最小,由牛顿第二定律可列式求解.
解答 解:(1)汽车转弯的速度 v=36km/h=10m/s
当转弯半径r=40m时,其所需的向心力 Fn=m$\frac{{v}^{2}}{r}$=2000×$\frac{1{0}^{2}}{40}$N=5000N
(2)当静摩擦力达到最大时汽车恰好不发生侧滑,则有
0.5mg=m$\frac{{v}^{2}}{{r}_{m}}$
可得最小的半径为 rm=$\frac{{v}^{2}}{0.5g}$=$\frac{1{0}^{2}}{5}$m=20m
答:(1)当转弯半径r=40m时,其所需的向心力为5000N.
(2)为保证汽车不发生侧滑,转弯半径至少是20m.
点评 解决本题的关键是分析向心力是由什么力提供的.通常这样找向心力:沿半径方向的所有力的合力提供该物体做圆周运动的向心力.

练习册系列答案
相关题目
18.在某一高度以v0=20m/s的初速度竖直上抛一个小球(不计空气阻力),当小球速度大小为10m/s时,以下判断不正确的是(g取10m/s 2)( )
| A. | 小球在这段时间内的平均速度大小可能为 5 m/s,方向向上 | |
| B. | 小球在这段时间内的平均速度大小可能为 15 m/s,方向向上 | |
| C. | 小球在这段时间内的平均速率大小可能为$\frac{25}{3}$m/s | |
| D. | 小球的路程大小一定是15m |
2.下列关于电磁波的说法正确的是( )
| A. | 只要空间有电场和磁场,就能激发出电磁波 | |
| B. | 各种电磁波在同种介质中传播速度相同 | |
| C. | 电磁波可以发生偏振现象 | |
| D. | 利用红外线进行遥感、遥控,主要是因为红外线的波长长,不容易发生衍射 |
19.在下列实例中(不计空气阻力)机械能守恒的是( )
| A. | 拉着一个物体沿着光滑的斜面匀速上升 | |
| B. | 物体沿光滑斜面自由下滑 | |
| C. | 物体做竖直上抛运动 | |
| D. | 竖直面内匀速圆周运动的小球 |
16.物体从静止开始做匀加速直线运动,已知第3s内与第2s内的位移之差是6m,则可知( )
| A. | 物体运动的加速度为3m/s2 | B. | 物体在前4s内的平均速度为15m/s | ||
| C. | 第1 s内的位移为3 m | D. | 第2s末的速度为12m/s |
17.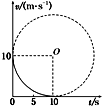 一个可视为质点的小滑块以10m/s的初速度沿直线做减速运动,在10s末速度减为0,滑块的v-t图象恰好是与两坐标轴相切的四分之一圆弧,如图所示,则该滑块在10s内的位移大小为( )
一个可视为质点的小滑块以10m/s的初速度沿直线做减速运动,在10s末速度减为0,滑块的v-t图象恰好是与两坐标轴相切的四分之一圆弧,如图所示,则该滑块在10s内的位移大小为( )
 一个可视为质点的小滑块以10m/s的初速度沿直线做减速运动,在10s末速度减为0,滑块的v-t图象恰好是与两坐标轴相切的四分之一圆弧,如图所示,则该滑块在10s内的位移大小为( )
一个可视为质点的小滑块以10m/s的初速度沿直线做减速运动,在10s末速度减为0,滑块的v-t图象恰好是与两坐标轴相切的四分之一圆弧,如图所示,则该滑块在10s内的位移大小为( )| A. | 100m | B. | 78.5m | C. | 50m | D. | 21.5m |
 一条长3L的绝缘细线穿过两个完全相同且质量都是m的小金属环A、B,将线的两端固定于同一点O,如图7所示,当金属环带电后,由于两环间的静电斥力使细线构成一等边三角形,此时两环恰恰处于同一水平线上.若不计环与线间的摩擦,则:
一条长3L的绝缘细线穿过两个完全相同且质量都是m的小金属环A、B,将线的两端固定于同一点O,如图7所示,当金属环带电后,由于两环间的静电斥力使细线构成一等边三角形,此时两环恰恰处于同一水平线上.若不计环与线间的摩擦,则: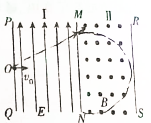 如图所示,在I区里有竖直方向的匀强电场E=4×105N/C,在Ⅱ区里有垂直于纸面向外的匀强磁场.电场和磁场的宽度d相等,d=0.4m.质荷比$\frac{m}{q}$=4×10-10kg/C的带正电的粒子,以初速度v0=2×107m/s从PQ边界上的O点垂直PQ射人电场.若电磁场在竖直方向足够长,不计粒子的重力,求:
如图所示,在I区里有竖直方向的匀强电场E=4×105N/C,在Ⅱ区里有垂直于纸面向外的匀强磁场.电场和磁场的宽度d相等,d=0.4m.质荷比$\frac{m}{q}$=4×10-10kg/C的带正电的粒子,以初速度v0=2×107m/s从PQ边界上的O点垂直PQ射人电场.若电磁场在竖直方向足够长,不计粒子的重力,求:


