题目内容
15.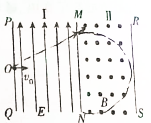 如图所示,在I区里有竖直方向的匀强电场E=4×105N/C,在Ⅱ区里有垂直于纸面向外的匀强磁场.电场和磁场的宽度d相等,d=0.4m.质荷比$\frac{m}{q}$=4×10-10kg/C的带正电的粒子,以初速度v0=2×107m/s从PQ边界上的O点垂直PQ射人电场.若电磁场在竖直方向足够长,不计粒子的重力,求:
如图所示,在I区里有竖直方向的匀强电场E=4×105N/C,在Ⅱ区里有垂直于纸面向外的匀强磁场.电场和磁场的宽度d相等,d=0.4m.质荷比$\frac{m}{q}$=4×10-10kg/C的带正电的粒子,以初速度v0=2×107m/s从PQ边界上的O点垂直PQ射人电场.若电磁场在竖直方向足够长,不计粒子的重力,求:(1)求粒子经过电场、磁场边界MN时的速度及偏离v0方向的距离;
(2)若要使粒子在磁场区域,不偏出RS边界,则磁感应强度B的取值范围;
(3)粒子在电、磁扬中的最长运动时间.
分析 (1)粒子在电场中做类平抛运动,应用类平抛运动规律可以求出粒子的速度、粒子的偏移量.
(2)粒子在磁场中做匀速圆周运动,求出粒子的轨道半径的临界值,然后由牛顿第二定律求出磁感应强度的临界值,最后确定磁感应强度范围.
(3)求出粒子在电场与磁场中的运动时间,然后求出粒子总的运动时间.
解答 解:(1)粒子在电场中做类平抛运动,
水平方向:d=v0t1,
解得:t1=2×10-8s,
竖直方向:vy=at1=$\frac{qE}{m}$t1,vy=2×107m/s,
粒子速度偏角的正切值:tanθ=$\frac{{v}_{y}}{{v}_{0}}$=1,则θ=45°,
粒子离开MN时的速度:v=$\sqrt{{v}_{0}^{2}+{v}_{y}^{2}}$=2$\sqrt{2}$×107m/s,
粒子的偏移量:y=$\frac{1}{2}$at12=$\frac{1}{2}$$\frac{qE}{m}$t12=0.2m;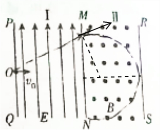 (2)粒子恰好不离开RS边界时的运动轨迹如图所示:
(2)粒子恰好不离开RS边界时的运动轨迹如图所示:
由几何知识得:rsin45°+r=d,
解得:r=(2-$\sqrt{2}$)d=0.4(2-$\sqrt{2}$)m,
粒子在磁场中做圆周运动,洛伦兹力提供向心力,由牛顿第二定律得:
qvB=m$\frac{{v}^{2}}{r}$,
解得:B=$\frac{mv}{qr}$=0.02(1+$\sqrt{2}$)T≈0.048T,
磁感应强度B的取值范围:B≥0.048T;
(3)粒子在磁场中做圆周运动的周期:T=$\frac{2πm}{qB}$,
粒子在磁场中做圆周运动的最长时间:
t2=$\frac{α}{360°}$T=$\frac{270°}{360°}$×$\frac{2πm}{qB}$=3.925×10-8s,
粒子的最长运动时间:t=t1+t2=5.925×10-8s;
答:(1)粒子经过电场、磁场边界MN时的速度大小为2$\sqrt{2}$×107m/s,与水平方向夹角为45°,偏离v0方向的距离为0.2m;
(2)若要使粒子在磁场区域,不偏出RS边界,磁感应强度B的取值范围是B≥0.048T;
(3)粒子在电、磁扬中的最长运动时间为:5.925×10-8s.
点评 本题考查了粒子在电场与磁场中的运动,分析清楚粒子运动过程、作出粒子运动轨迹是解题的关键,应用类平抛运动规律、牛顿第二定律与粒子做圆周运动的周期公式可以解题.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案| A. | 布朗运动就是液体分子的无规则运动 | |
| B. | 当两分子间距离增大时,分子力一定减小而分子势能一定增加 | |
| C. | 一定量100℃的水变成100℃的水蒸气,其分子之间的势能增加 | |
| D. | 温度降低,物体内所有分子运动的速度不一定都变小 |
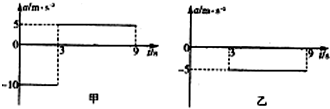
| A. | t=6s时两车等速 | B. | t=6s时两车距离最远 | ||
| C. | 0-6s内两车位移之差为90m | D. | 两车0-9s在内会相撞 |
| A. | 铁的密度 | B. | 铁的相对原子质量 | ||
| C. | 某铁块的质量和体积 | D. | 铁的密度和铁原子的摩尔质量 |
| A. | 如果重力对物体做正功,则物体的重力势能增大 | |
| B. | 如果重力对物体做正功,则物体的重力势能减小 | |
| C. | 物体的重力势能具有相对性,与参考平面的选取有关 | |
| D. | 重力势能是物体与地球组成的系统具有的,而不是物体单独具有的 |
| A. | 3s内的位移是12m | B. | 3s内的位移是9m | ||
| C. | 3s末速度的大小是0 | D. | 3s末速度的大小是6m/s |
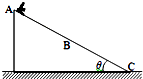 如图所示是放置于水平地面上的简易滑梯示意图,一小孩从滑梯斜面顶点A开始无初速度下滑,在AB段匀加速下滑,在BC段匀减速下滑,滑到C点恰好速度为零(B点为AC的中点),整个过程中滑梯保持静止状态.假设该小孩在AB段和BC段滑动时与斜面间的动摩擦因数分别为μ1和μ2,斜面倾角为θ,则下列说法正确的是( )
如图所示是放置于水平地面上的简易滑梯示意图,一小孩从滑梯斜面顶点A开始无初速度下滑,在AB段匀加速下滑,在BC段匀减速下滑,滑到C点恰好速度为零(B点为AC的中点),整个过程中滑梯保持静止状态.假设该小孩在AB段和BC段滑动时与斜面间的动摩擦因数分别为μ1和μ2,斜面倾角为θ,则下列说法正确的是( )| A. | 小孩在AB段和BC段运动过程中速度改变量相同 | |
| B. | 小孩在AB段和BC段运动过程中重力的平均功率相同 | |
| C. | 动摩擦因数满足μ1+μ2=2tanθ | |
| D. | 整个过程中地面对滑梯的支持力始终等于该小孩和滑梯的总重力,地面对滑梯始终无摩擦力作用 |