题目内容
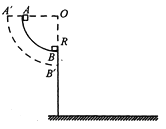
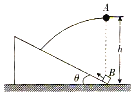
【题目】如图所示，在水平地面上有一倾角为θ的光滑固定斜面，在斜面底端的正上方高度为h处平抛一小球A，同时在斜面底端一物块B以某一初速度沿斜面上滑，当其滑到最高点时恰好与小球A相遇，小球A和物块B均视为质点，忽略空气阻力，重力加速度为g，则下列判断正确的是（ ）
A. 物块B沿斜面上滑的初速度为
B. 物块B沿斜面上滑的高度
h
C. 小球A在空中运动的时间为
D. 小球A水平抛出时的初速度为sinθcosθ
【答案】BD
【解析】
物块沿斜面向上做匀减速运动，根据牛顿第二定律求出B上滑的加速度，通过运动学公式求出上滑的时间和位移，从而得出A平抛运动的水平位移，结合时间求出B的初速度．根据平抛运动的规律求A的初速度．
根据牛顿第二定律得，B上滑的加速度为：
，B上滑的最大位移为：
，运动的时间
，对于A球，有：
，因为
，所以联立得：
，解得B沿斜面上滑的初速度为：
，故A错误。物体B上滑的高度
，故B正确。小球A在空中运动的时间为：
，故C错误。因为
，小球A水平抛出时的初速度为：
，且，联立解得：
，故D正确。故选BD。
练习册系列答案
阅读快车系列答案
相关题目
