题目内容
19．已知货物的质量为m，在某段时间内起重机将货物以a的加速度加速升高h，则在这段时间内叙述正确的是（重力加速度为g）（ ）| A． | 货物的机械能一定增加mah+mgh | B． | 货物的机械能一定增加mah | ||
| C． | 货物的重力势能一定增加mgh | D． | 货物的动能一定增加mah-mgh |
分析 重力势能的增量等于货物克服重力做功；根据动能定理求解动能的增量；机械能等于重力势能与动能之和，由这两种能的变化，即可确定机械能的增量．
解答 解：货物上升高度为h，则货物克服重力做功为mgh，则重力势能增加一定为mgh．故C正确；
由动能定理得：△Ek=W合=F合h=mah，故货物动能增加一定为mah．故D错误．
因机械能等于重力势能与动能之和，由上分析知，重力势能增加mgh，动能增加为mah，则货物的机械能一定增加mah+mgh．故A正确，B错误．
故选：AC
点评 本题考查了恒力做功引起物体动能变化的过程，正确分析功和能的关系解题的关键．明确重力做功一定等于重力势能的改变量；合外力做功一定等于动能的改变量．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
9．
如图所示，两束单色光a、b从水面下射向A点，光线经折射后合成一束光c，则下列说法正确的是（ ）
如图所示，两束单色光a、b从水面下射向A点，光线经折射后合成一束光c，则下列说法正确的是（ ）| A． | 用同一双缝干涉实验装置分别以a、b光做实验，a光的干涉条纹间距大于b光的干涉条纹间距 | |
| B． | 用a、b光分别做单缝衍射实验时它们的衍射条纹宽度都是均匀的 | |
| C． | 在水中a光的速度比b光的速度小 | |
| D． | 从水射向空气时a光的临界角大于b光的临界角 |
10．
一多用电表的表盘如图所示，该表先正确测量了一个阻值约为20Ω的电阻，若再測量一个阻值约为2kΩ的电阻．此时选择开关应选择欧姆挡的（ ）位置．
一多用电表的表盘如图所示，该表先正确测量了一个阻值约为20Ω的电阻，若再測量一个阻值约为2kΩ的电阻．此时选择开关应选择欧姆挡的（ ）位置．| A． | ×1 | B． | ×1OO | C． | ×1k | D． | ×1OO或×1k |
14．
2011年11月，神舟八号与天宫一号完美“牵手”，成功实现交会对接（如图）．交会对接飞行过程分为远距离导引段、自主控制段、对接段、组合体飞行段和分离撤离段．任务完成后，神舟八号飞船返同位于内蒙古自治区的主着陆场．则下列说法正确的是（ ）
2011年11月，神舟八号与天宫一号完美“牵手”，成功实现交会对接（如图）．交会对接飞行过程分为远距离导引段、自主控制段、对接段、组合体飞行段和分离撤离段．任务完成后，神舟八号飞船返同位于内蒙古自治区的主着陆场．则下列说法正确的是（ ）| A． | 在远距离导引段，神舟八号应在距天宫一号目标飞行器前下方某处 | |
| B． | 在远距离导引段，神舟八号应在距天宫一号目标飞行器后下方某处 | |
| C． | 在组合体飞行段，神舟八号与天宫一号绕地球作匀速圆周运动的速度小于7.9km/s | |
| D． | 分离后，天宫一号变轨升高至飞行轨道运行时，其动能比在交会对接轨道时大 |
4．
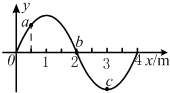一列简谐波沿x轴正方向传播，传播速度v=200m/s，t=0时刻波形如图所示，a、b、c为波传播方向上的三点，平衡位置的坐标分别为（0.5m，2m，3m）．下列说法正确的是（ ）
一列简谐波沿x轴正方向传播，传播速度v=200m/s，t=0时刻波形如图所示，a、b、c为波传播方向上的三点，平衡位置的坐标分别为（0.5m，2m，3m）．下列说法正确的是（ ）| A． | 此时刻质点b正向y轴的负方向运动 | |
| B． | 该简谐波的频率为50Hz | |
| C． | t=0.05s时，质点b在y轴正方向最大位移处 | |
| D． | 经0.0175s，质点a在y正方向最大位移处 |
11．下列关于热现象的说法，正确的是（ ）
| A． | 分子间距离减小，分子势能一定减小 | |
| B． | 只要知道气体的摩尔体积和阿伏加德罗常数，就可以算出气体分子的体积 | |
| C． | 气体的温度升高，个别气体分子运动的速率可能减小 | |
| D． | 对一定质量的理想气体，在等温变化时，内能不改变，因而与外界不发生热交换 |
3．
如图所示为某种质谱仪的工作原理示意图．此质谱仪由以下几部分构成：粒子源N；P、Q间的加速电场；静电分析器，即中心线半径为R的四分之一圆形通道，通道内有均匀辐射电场，方向沿径向指向圆心O，且与圆心O等距的各点电场强度大小相等；磁感应强度为B的有界匀强磁场，方向垂直纸面向外；胶片M．由粒子源发出的各种不同带电粒子中有质子（${\;}_{1}^{1}$H）、氚核（${\;}_{1}^{2}$H）和α粒子（${\;}_{2}^{4}$He），经加速电场加速后进入静电分析器，这些粒子能沿中心线通过静电分析器并经小孔S垂直磁场边界进入磁场，最终打到胶片上．粒子从粒子源发出时的初速度不同，不计粒子所受重力．下列说法中正确的是（ ）
如图所示为某种质谱仪的工作原理示意图．此质谱仪由以下几部分构成：粒子源N；P、Q间的加速电场；静电分析器，即中心线半径为R的四分之一圆形通道，通道内有均匀辐射电场，方向沿径向指向圆心O，且与圆心O等距的各点电场强度大小相等；磁感应强度为B的有界匀强磁场，方向垂直纸面向外；胶片M．由粒子源发出的各种不同带电粒子中有质子（${\;}_{1}^{1}$H）、氚核（${\;}_{1}^{2}$H）和α粒子（${\;}_{2}^{4}$He），经加速电场加速后进入静电分析器，这些粒子能沿中心线通过静电分析器并经小孔S垂直磁场边界进入磁场，最终打到胶片上．粒子从粒子源发出时的初速度不同，不计粒子所受重力．下列说法中正确的是（ ）| A． | 从小孔S进入磁场的质子、氚核和α粒子速度大小一定相等 | |
| B． | 从小孔S进入磁场的质子、氚核和α粒子动能一定相等 | |
| C． | 质子、氚核和α粒子打到胶片上三个不同点，α粒子距离O点最近 | |
| D． | 质子、氚核和α粒子打到胶片上两个不同点，质子距离O点最近 |
4．
可拆变压器可简化成如图的模型，MN为可拆的铁芯横条，P1、P2为横条与固定铁芯的间隙，压紧横条，当间隙P1、P2为零时，变压器可视为理想变压器．将变压器的初级接到电压为U1的正弦交流电源上，在间隙P1、P2逐渐减小的过程中，下列说法正确的是（ ）
可拆变压器可简化成如图的模型，MN为可拆的铁芯横条，P1、P2为横条与固定铁芯的间隙，压紧横条，当间隙P1、P2为零时，变压器可视为理想变压器．将变压器的初级接到电压为U1的正弦交流电源上，在间隙P1、P2逐渐减小的过程中，下列说法正确的是（ ）| A． | 次级输出电压的频率越来越高 | |
| B． | 次级的输出电压越来越大 | |
| C． | 输入、输出电压与匝数的关系始终满足$\frac{{U}_{1}}{{U}_{2}}$=$\frac{{n}_{1}}{{n}_{2}}$ | |
| D． | 当P1、P2为零时，$\frac{{U}_{1}}{{U}_{2}}$=$\frac{{n}_{1}}{{n}_{2}}$ |