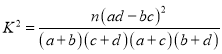【题目】将某公司200天的日销售收入(单位:万元)统计如下表(1)所示,
日销售收入 |
|
|
|
|
|
|
频数 | 12 | 28 | 36 | 54 | 50 | 20 |
频率 |
表(1)
(1)完成上述频率分布表,并估计公司这200天的日均销售收入(同一组中的数据用该组所在区间的中点值代表);
(2)已知该公司2020年第一、二季度的日销售收入如下表(2)所示,第三季度的日销售收入及其频率可用表(1)中的数据近似代替,且在2020年,当公司日销售收入为![]() 时,员工的日绩效为100元,当公司日销售收入为
时,员工的日绩效为100元,当公司日销售收入为![]() 时,员工的日绩效为200元,当公司日销售收入为
时,员工的日绩效为200元,当公司日销售收入为![]() 时,员工的日绩效为300元.以频率估计概率.
时,员工的日绩效为300元.以频率估计概率.
①若在第三季度某员工的工作日中随机抽取2天,记该员工2天的绩效之和为![]() ,求
,求![]() 的分布列以及数学期望;
的分布列以及数学期望;
②若每个员工每个季度的工作日为50天,估计2020年前三个季度每个员工获得的绩效的总额.
日销售收入 |
|
|
|
|
|
|
频率 | 0.2 | 0.3 | 0.2 | 0.1 | 0.1 | 0.1 |
表(2)
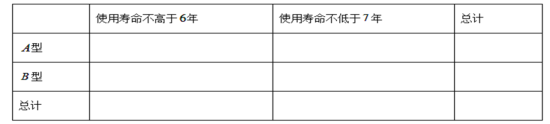
【题目】在全面抗击新冠肺炎疫情这一特殊时期,我市教育局提出“停课不停学”的口号,鼓励学生线上学习.某校数学教师为了调查高三学生数学成绩与线上学习时间之间的相关关系,对高三年级随机选取45名学生进行跟踪问卷,其中每周线上学习数学时间不少于5小时的有19人,余下的人中,在检测考试中数学平均成绩不足120分的占![]() ,统计成绩后得到如下
,统计成绩后得到如下![]() 列联表:
列联表:
分数不少于120分 | 分数不足120分 | 合计 | |
线上学习时间不少于5小时 | 4 | 19 | |
线上学习时间不足5小时 | |||
合计 | 45 |
(1)请完成上面![]() 列联表;并判断是否有99%的把握认为“高三学生的数学成绩与学生线上学习时间有关”;
列联表;并判断是否有99%的把握认为“高三学生的数学成绩与学生线上学习时间有关”;
(2)①按照分层抽样的方法,在上述样本中从分数不少于120分和分数不足120分的两组学生中抽取9名学生,设抽到不足120分且每周线上学习时间不足5小时的人数是![]() ,求
,求![]() 的分布列(概率用组合数算式表示);
的分布列(概率用组合数算式表示);
②若将频率视为概率,从全校高三该次检测数学成绩不少于120分的学生中随机抽取20人,求这些人中每周线上学习时间不少于5小时的人数的期望和方差.
(下面的临界值表供参考)
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式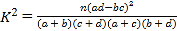 其中
其中![]() )
)