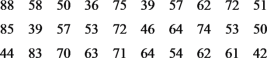题目内容
【题目】设椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,椭圆
,椭圆![]() 上一点
上一点![]() 到左右两个焦点
到左右两个焦点![]() 、
、![]() 的距离之和是4.
的距离之和是4.
(1)求椭圆的方程;
(2)已知过![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 、
、![]() 两点,且两点与左右顶点不重合,若
两点,且两点与左右顶点不重合,若![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ;(2)6.
;(2)6.
【解析】
(1)首先可根据题意得出![]() ,然后根据
,然后根据![]() 得出
得出![]() ,最后通过
,最后通过![]() 计算出
计算出![]() 的值并写出椭圆
的值并写出椭圆![]() 方程;
方程;
(2)首先可以设![]() 、
、![]() ,然后根据直线过点
,然后根据直线过点![]() 设出直线
设出直线![]() 方程,再然后联立直线方程与椭圆方程,根据韦达定理得出
方程,再然后联立直线方程与椭圆方程,根据韦达定理得出![]() 以及
以及![]() ,再然后结合题意得出四边形
,再然后结合题意得出四边形![]() 是平行四边形以及其面积
是平行四边形以及其面积![]() ,最后通过计算即可得出结果.
,最后通过计算即可得出结果.
(1)因为椭圆![]() 上一点
上一点![]() 到左右两个焦点
到左右两个焦点![]() 、
、![]() 的距离之和是4,
的距离之和是4,
所以![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() ,
,![]()
所以椭圆C方程为![]() .
.
(2)设![]() ,
,![]() ,
,
因为直线过点![]() ,所以可设直线
,所以可设直线![]() 方程为
方程为![]() ,
,
联立方程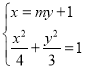 ,消去
,消去![]() 可得:
可得:![]() ,
,
化简整理得![]() ,
,
其中![]() ,
,
![]() ,
,![]() ,
,
因为![]() ,所以四边形
,所以四边形![]() 是平行四边形,
是平行四边形,
设平面四边形![]() 的面积为
的面积为![]() ,
,
则![]() ,
,
设![]() ,则
,则![]() ,
,
所以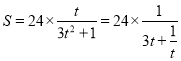 ,
,
因为![]() ,所以
,所以![]() ,
,![]() ,
,
所以四边形![]() 面积的最大值为6.
面积的最大值为6.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
【题目】某医院用光电比色计检查尿汞时,得尿汞含量(毫克/升)与消光系数如下表:
尿汞含量 | 2 | 4 | 6 | 8 | 10 |
消光系数 | 64 | 138 | 205 | 285 | 360 |
(1)作散点图;
(2)如果![]() 与
与![]() 之间具有线性相关关系,求回归线直线方程;
之间具有线性相关关系,求回归线直线方程;
(3)估计尿汞含量为9毫克/升时消光系数.
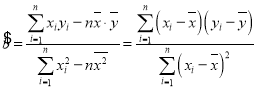 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.