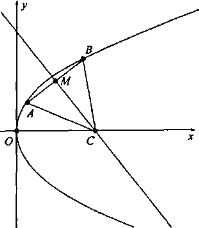
【题目】某市政府为了引导居民合理用水,决定全面实施阶梯水价,居民用水原则上以住宅为单位(一套住宅为一户).
阶梯级别 | 第一阶梯 | 第二阶梯 | 第三阶梯 |
月用水范围(吨) |
|
|
|
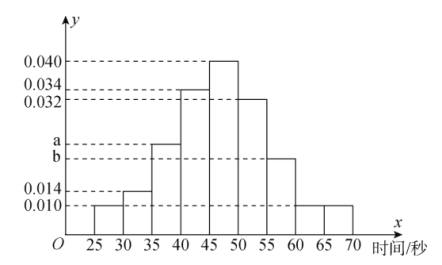
为了了解全市居民月用水量的分布情况,通过抽样,获得了![]() 户居民的月用水量(单位:吨),得到统计表如下:
户居民的月用水量(单位:吨),得到统计表如下:
居民用水户编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
用水量(吨) | 7 | 8 | 8 | 9 | 10 | 11 | <>13 | 14 | 15 | 20 |
(1)若用水量不超过![]() 吨时,按
吨时,按![]() 元/吨计算水费;若用水量超过
元/吨计算水费;若用水量超过![]() 吨且不超过
吨且不超过![]() 吨时,超过
吨时,超过![]() 吨部分按
吨部分按![]() 元/吨计算水费;若用水量超过
元/吨计算水费;若用水量超过![]() 吨时,超过
吨时,超过![]() 吨部分按
吨部分按![]() 元/吨计算水费.试计算:若某居民用水
元/吨计算水费.试计算:若某居民用水![]() 吨,则应交水费多少元?
吨,则应交水费多少元?
(2)现要在这![]() 户家庭中任意选取
户家庭中任意选取![]() 户,求取到第二阶梯水量的户数的分布列与期望;
户,求取到第二阶梯水量的户数的分布列与期望;
(3)用抽到的![]() 户家庭作为样本估计全市的居民用水情况,从全市依次随机抽取
户家庭作为样本估计全市的居民用水情况,从全市依次随机抽取![]() 户,若抽到
户,若抽到![]() 户月用水量为第一阶梯的可能性最大,求
户月用水量为第一阶梯的可能性最大,求![]() 的值.
的值.
【题目】某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
积极参加 班级工作 | 不太主动参加 班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性一般 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验的思想方法能否有99.9%的把握认为学生的学习积极性与对待班级工作的态度有关系?并说明理由.(参考下表)
P(K2 ≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | |
k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: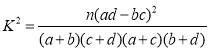 ,其中
,其中![]() )
)
【题目】有人收集了七月份的日平均气温![]() (摄氏度)与某次冷饮店日销售额
(摄氏度)与某次冷饮店日销售额![]() (百元)的有关数据,为分析其关系,该店做了五次统计,所得数据如下:
(百元)的有关数据,为分析其关系,该店做了五次统计,所得数据如下:
日平均气温 | 31 | 32 | 33 | 34 | 35 |
日销售额 | 5 | 6 | 7 | 8 | 10 |
由资料可知,![]() 关于
关于![]() 的线性回归方程是
的线性回归方程是![]() ,给出下列说法:
,给出下列说法:
①![]() ;
;
②日销售额![]() (百元)与日平均气温
(百元)与日平均气温![]() (摄氏度)成正相关;
(摄氏度)成正相关;
③当日平均气温为![]() 摄氏度时,日销售额一定为
摄氏度时,日销售额一定为![]() 百元.
百元.
其中正确说法的序号是______.