题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,设
时,设![]() ,
,![]() 为
为![]() 的两个不同极值点,证明:
的两个不同极值点,证明:![]() ;
;
(2)设![]() ,
,![]() 为
为![]() 的两个不同零点,证明:
的两个不同零点,证明:![]() .
.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)求出函数![]() 的导函数
的导函数![]() ,
,![]() ,
,![]() 为
为![]() 的两个不同极值点,转化为
的两个不同极值点,转化为![]() 为方程
为方程![]() 的两不等正根,再利用韦达定理和基本不等式即可证明;
的两不等正根,再利用韦达定理和基本不等式即可证明;
(2)要证明![]() ,只要证明
,只要证明![]() 和
和![]() ,分别利用导数进行证明即可.
,分别利用导数进行证明即可.
(1)当![]() 时,
时,![]() ,
,
![]() ,
,
![]() 为
为![]() 的两个不同极值点,
的两个不同极值点,
![]() 为方程
为方程![]() 的两不等正根,
的两不等正根,
![]() ,
,
且由韦达定理![]() ,
,
![]()
![]()
![]() ,
,
![]() .
.
(2)要证明![]() ,
,
即![]() ,
,
下面分别证明![]() 和
和![]() ,
,
两式相加即得结论.
(i)![]() ,
,
令![]() ,
,
即证![]() .
.
令函数![]() ,则
,则![]() ,
,
![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,
单调递减,
![]() .
.
(ii)再证明![]() ,
,
即![]() .
.
![]() 为
为![]() 的两个不同零点,不妨设
的两个不同零点,不妨设![]() ,
,
![]() ①
①
![]() ②
②
![]() ①-②可得
①-②可得![]() ,
,
两边同时乘以![]() ,
,
可得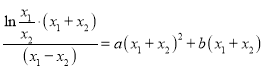 ,
,
即 .
.
令![]() ,则
,则![]() .
.
即证![]() ,
,
即![]() ,
,
即证![]() .
.
令函数![]() ,
,
则![]() ,
,
![]() 在
在![]() 单调递增,
单调递增,
![]() .
.
由(i)(ii)可得![]() ,
,
![]() .
.

【题目】某市创卫办为了了解该市开展创卫活动的成效,对市民进行了一次创卫满意程度测试,根据测试成绩评定“合格”、“不合格”两个等级,同时对相应等级进行量化:“合格”计5分,“不合格”计0分,现随机抽取部分市民的回答问卷,统计结果及对应的频率分布直方图如图所示:
等级 | 不合格 | 合格 | ||
得分 |
|
|
|
|
频数 | 6 |
| 24 |
|

(1)求![]() 的值;
的值;
(2)按照分层抽样的方法,从评定等级为“合格”和“不合格”的问卷中随机抽取10份进行问题跟踪调研,现再从这10份问卷中任选4份,记所选4份问卷的量化总分为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() ;
;
(3)某评估机构以指标![]() (
(![]() ,其中
,其中![]() 表示
表示![]() 的方差)来评估该市创卫活动的成效.若
的方差)来评估该市创卫活动的成效.若![]() ,则认定创卫活动是有效的;否则认为创卫活动无效,应该调整创卫活动方案.在(2)的条件下,判断该市是否应该调整创卫活动方案?
,则认定创卫活动是有效的;否则认为创卫活动无效,应该调整创卫活动方案.在(2)的条件下,判断该市是否应该调整创卫活动方案?
【题目】2019年11月份,全国工业生产者出厂价格同比下降![]() ,环比下降
,环比下降![]() 某企业在了解市场动态之后,决定根据市场动态及时作出相应调整,并结合企业自身的情况作出相应的出厂价格,该企业统计了2019年1~10月份产品的生产数量
某企业在了解市场动态之后,决定根据市场动态及时作出相应调整,并结合企业自身的情况作出相应的出厂价格,该企业统计了2019年1~10月份产品的生产数量![]() (单位:万件)以及销售总额
(单位:万件)以及销售总额![]() (单位:十万元)之间的关系如下表:
(单位:十万元)之间的关系如下表:
| 2.08 | 2.12 | 2.19 | 2.28 | 2.36 | 2.48 | 2.59 | 2.68 | 2.80 | 2.87 |
| 4.25 | 4.37 | 4.40 | 4.55 | 4.64 | 4.75 | 4.92 | 5.03 | 5.14 | 5.26 |
(1)计算![]() 的值;
的值;
(2)计算相关系数![]() ,并通过
,并通过![]() 的大小说明
的大小说明![]() 与
与![]() 之间的相关程度;
之间的相关程度;
(3)求![]() 与
与![]() 的线性回归方程
的线性回归方程![]() ,并推测当产量为3.2万件时销售额为多少.(该问中运算结果保留两位小数)
,并推测当产量为3.2万件时销售额为多少.(该问中运算结果保留两位小数)
附:回归直线方程![]() 中的斜率和截距的最小二乘估计公式分别为
中的斜率和截距的最小二乘估计公式分别为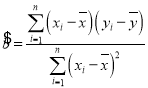 ,
,![]() ;
;
相关系数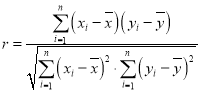 .
.
参考数据: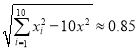 ,
,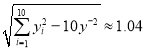 ,
,![]() .
.