12.在复平面内,复数$\frac{-2-3i}{i}$对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
11.下列各数中最小的数是( )
| A. | 111 111(2) | B. | 210(6) | C. | 1 000(4) | D. | 110(8) |
10.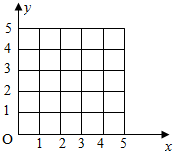 某车间为了规定工时定额,需要确定加工某零件所花费的时间,为此作了四次实验,得到的数据如下:
某车间为了规定工时定额,需要确定加工某零件所花费的时间,为此作了四次实验,得到的数据如下:
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出y关于x的线性回归方程;
(3)试预测加工10个零件需要多少时间?(注:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\stackrel{∧}{y}$-$\stackrel{∧}{b}$$\overline{x}$)
 某车间为了规定工时定额,需要确定加工某零件所花费的时间,为此作了四次实验,得到的数据如下:
某车间为了规定工时定额,需要确定加工某零件所花费的时间,为此作了四次实验,得到的数据如下:| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
(2)求出y关于x的线性回归方程;
(3)试预测加工10个零件需要多少时间?(注:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\stackrel{∧}{y}$-$\stackrel{∧}{b}$$\overline{x}$)
9.已知四边形ABCD是椭圆$\frac{{x}^{2}}{4}$+y2=1的内接菱形,则四边形ABCD的内切圆方程是( )
| A. | x2+y2=$\frac{1}{5}$ | B. | (x-1)2+y2=$\frac{2}{5}$ | C. | x2+y2=$\frac{4}{5}$ | D. | x2+y2=$\frac{3}{5}$ |
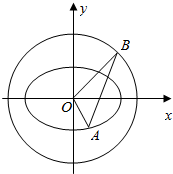
5.已知A 为椭圆上一点,E,F 分别为椭圆的左右焦点,∠EAF=90°,设AE 的延长线交椭圆于B,又|AB|=|AF|,则椭圆的离心率e为( )
0 252104 252112 252118 252122 252128 252130 252134 252140 252142 252148 252154 252158 252160 252164 252170 252172 252178 252182 252184 252188 252190 252194 252196 252198 252199 252200 252202 252203 252204 252206 252208 252212 252214 252218 252220 252224 252230 252232 252238 252242 252244 252248 252254 252260 252262 252268 252272 252274 252280 252284 252290 252298 266669
| A. | $\sqrt{6}$-$\sqrt{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{5}-1}{2}$ | D. | $\frac{\sqrt{5}-\sqrt{2}}{2}$ |
 如图,O为坐标原点,A和B分别是椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1( a>b>0)和C2:$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{{n}^{2}}$=1(m>n>0)上的动点,满足$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,且椭圆C2的离心率为$\frac{\sqrt{2}}{2}$.当动点A在x轴上的投影恰为C的右焦点F时,有S△AOF=$\frac{\sqrt{2}}{4}$
如图,O为坐标原点,A和B分别是椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1( a>b>0)和C2:$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{{n}^{2}}$=1(m>n>0)上的动点,满足$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,且椭圆C2的离心率为$\frac{\sqrt{2}}{2}$.当动点A在x轴上的投影恰为C的右焦点F时,有S△AOF=$\frac{\sqrt{2}}{4}$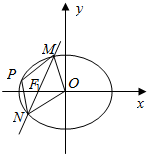 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴长为8,且离心率为$\frac{{\sqrt{2}}}{2}$.
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴长为8,且离心率为$\frac{{\sqrt{2}}}{2}$. 如图,在平面直角坐标系xoy中,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为e=$\frac{\sqrt{3}}{2}$,过椭圆由焦点F作两条互相垂直的弦AB与CD.当直线AB斜率为0时,弦AB长4.
如图,在平面直角坐标系xoy中,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为e=$\frac{\sqrt{3}}{2}$,过椭圆由焦点F作两条互相垂直的弦AB与CD.当直线AB斜率为0时,弦AB长4.