题目内容
3.已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)过点$({1,\frac{{\sqrt{2}}}{2}})$,离心率为$\frac{{\sqrt{2}}}{2}$.(1)求椭圆C的方程;
(2)已知直线l1过椭圆C的右焦点F2交C于 M,N两点,点Q为直线l2:x=2上的点,且F2Q⊥l1,记直线MN与直线 OQ(O为原点)的交点为K,证明:MK=NK.
分析 (1)由题意可得:$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{2}}{2}}\\{{a}^{2}={b}^{2}+{c}^{2}}\\{\frac{1}{{a}^{2}}+\frac{1}{2{b}^{2}}=1}\end{array}\right.$,解出即可得出;
(2)设直线MN的方程为:x=my+1,M(x1,y1),N(x2,y2).与椭圆方程联立化为(2+m2)y2+2my-1=0,可得y1+y2.可得线段MN的中点坐标.由F2Q⊥l1,可得直线F2Q的方程为y=-m(x-1),可得Q与直线OQ的方程,只要证明线段MN的中点坐标满足上述方程即可.
解答 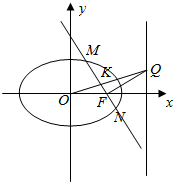 解:(1)由题意可得:$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{2}}{2}}\\{{a}^{2}={b}^{2}+{c}^{2}}\\{\frac{1}{{a}^{2}}+\frac{1}{2{b}^{2}}=1}\end{array}\right.$,解得a2=2,b=c=1.∴椭圆C的方程为$\frac{{x}^{2}}{2}+{y}^{2}$=1.
解:(1)由题意可得:$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{2}}{2}}\\{{a}^{2}={b}^{2}+{c}^{2}}\\{\frac{1}{{a}^{2}}+\frac{1}{2{b}^{2}}=1}\end{array}\right.$,解得a2=2,b=c=1.∴椭圆C的方程为$\frac{{x}^{2}}{2}+{y}^{2}$=1.
(2)设直线MN的方程为:x=my+1,M(x1,y1),N(x2,y2).
联立$\left\{\begin{array}{l}{x=my+1}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,化为(2+m2)y2+2my-1=0,y1+y2=$\frac{-2m}{2+{m}^{2}}$.
∴线段MN的中点坐标为$(\frac{2}{2+{m}^{2}},\frac{-m}{2+{m}^{2}})$.
∵F2Q⊥l1,∴直线F2Q的方程为y=-m(x-1),
∴Q(2,-m),
∴直线OQ的方程为:y=-$\frac{m}{2}$x,
∵线段MN的中点坐标$(\frac{2}{2+{m}^{2}},\frac{-m}{2+{m}^{2}})$满足上述方程.
∴MK=KN.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、一元二次方程的根与系数的关系、中点坐标公式、相互垂直的直线斜率之间的关系,考查了推理能力与计算能力,属于难题.

| A. | 9-$\sqrt{2}$ | B. | 3+$\sqrt{2}$ | C. | 6-$\sqrt{2}$ | D. | 6+$\sqrt{2}$ |
| x | 0 | 0.25 | 0.375 | 0.4065 | 0.438 |
| f(x) | -2 | -0.984 | -0.260 | -0.052 | -0.165 |
| x | 0.5 | 0.625 | 0.75 | 0.875 | 1 |
| f(x) | 0.625 | 1.982 | 2.645 | 4.35 | 6 |
| A. | 5个 | B. | 6个 | C. | 7个 | D. | 8个 |
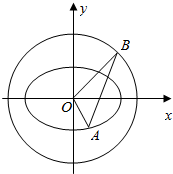 如图,O为坐标原点,A和B分别是椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1( a>b>0)和C2:$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{{n}^{2}}$=1(m>n>0)上的动点,满足$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,且椭圆C2的离心率为$\frac{\sqrt{2}}{2}$.当动点A在x轴上的投影恰为C的右焦点F时,有S△AOF=$\frac{\sqrt{2}}{4}$
如图,O为坐标原点,A和B分别是椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1( a>b>0)和C2:$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{{n}^{2}}$=1(m>n>0)上的动点,满足$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,且椭圆C2的离心率为$\frac{\sqrt{2}}{2}$.当动点A在x轴上的投影恰为C的右焦点F时,有S△AOF=$\frac{\sqrt{2}}{4}$