10.某工人生产合格零售的产量逐月增长,前5个月的产量如表所示:
(I)若从这5组数据中抽出两组,求抽出的2组数据恰好是相邻的两个月数据的概率;
(Ⅱ)请根据所给5组数据,求出 y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$;并根据线性回归方程预测该工人第6个月生产的合格零件的件数.
(附:回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$;$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$)
| 月份x | 1 | 2 | 3 | 4 | 5 |
| 合格零件y(件) | 50 | 60 | 70 | 80 | 100 |
(Ⅱ)请根据所给5组数据,求出 y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$;并根据线性回归方程预测该工人第6个月生产的合格零件的件数.
(附:回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$;$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$)
5.设α,β是方程x2-2mx+2-m=0(x∈R)的两个实根,则α2+β2的最小值为( )
| A. | 2 | B. | 0 | C. | 16 | D. | -$\frac{17}{4}$ |
4.函数y=$\frac{2x-1}{x+1}$(x>0)的值域为 ( )
| A. | (-,+∞) | B. | (-1,2) | C. | {y|y≠2} | D. | {y|y>2} |
3.已知集合A={-2,-1,0,1,2},B={x|-2<x<1},则A∩B=( )
0 251667 251675 251681 251685 251691 251693 251697 251703 251705 251711 251717 251721 251723 251727 251733 251735 251741 251745 251747 251751 251753 251757 251759 251761 251762 251763 251765 251766 251767 251769 251771 251775 251777 251781 251783 251787 251793 251795 251801 251805 251807 251811 251817 251823 251825 251831 251835 251837 251843 251847 251853 251861 266669
| A. | {-1,0} | B. | {0,1} | C. | {-1,0,1} | D. | {0,1,2} |
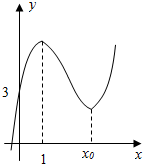 已知函数f(x)=ax3+bx2+(c-3a-2b)x+d(a>0)的图象如图.
已知函数f(x)=ax3+bx2+(c-3a-2b)x+d(a>0)的图象如图.