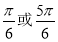7.对于函数f(x)=$\frac{x-1}{x+1}$,设f2(x)=f[f(x)],f3(x)=f[f2(x)],…,fn+1(x)=f[fn(x)](n∈N*,且n≥2),令集合M={x|f2015(x)=-x,x∈R},则集合M为( )
| A. | 空集 | B. | 实数集 | C. | 单元素集 | D. | 二元素集 |
5.定义在R上的偶函数f(x)满足f(x+1)=-f(x),且在[0,1]上单调递增,设a=f(3),b=f($\sqrt{2}$),c=f(2),则a,b,c大小关系是( )
| A. | b>c>a | B. | a>c>b | C. | a>b>c | D. | c>b>a |
2.已知$a={5^{-\frac{1}{2}}}$,b=ln2,c=log32,则( )
0 251333 251341 251347 251351 251357 251359 251363 251369 251371 251377 251383 251387 251389 251393 251399 251401 251407 251411 251413 251417 251419 251423 251425 251427 251428 251429 251431 251432 251433 251435 251437 251441 251443 251447 251449 251453 251459 251461 251467 251471 251473 251477 251483 251489 251491 251497 251501 251503 251509 251513 251519 251527 266669
| A. | a>b>c | B. | b>c>a | C. | c>b>a | D. | b>a>c |
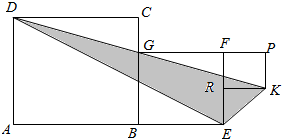 正方形ABCD、正方形BEFG和正方形RKPF的位置如图所示,点G在线段DK上,正方形BEFG的边长为4,则△DEK的面积为( )
正方形ABCD、正方形BEFG和正方形RKPF的位置如图所示,点G在线段DK上,正方形BEFG的边长为4,则△DEK的面积为( ) 是等差数列,
是等差数列,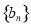 是等比数列,若
是等比数列,若 ,则( )A.
,则( )A. B.
B.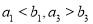
 D.
D.
 为等差数列,其公差为-2,且
为等差数列,其公差为-2,且 是
是 与
与 的等比中项,
的等比中项, 为
为 项和,则
项和,则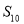 的值为( )
的值为( ) 中,角
中,角 所对的边分别为
所对的边分别为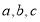 .若
.若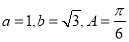 ,则角
,则角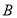 等于( )
等于( )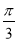 B.
B.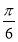 C.
C.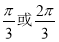 D.
D.