题目内容
1.已知数列{an},a1=1,a2=2,an+1-3an+2an-1=0,(n∈N*,且n≥2),求an,并求出它的前n项的和Sn.分析 由题意可得an+1-an=2(an-an-1),数列{an-an-1}为首项为1,公比为2的等比数列,运用等比数列的通项公式和数列恒等式an=a1+(a2-a1)+(a3-a2)+…+(an-an-1),再由等比数列的求和公式,即可得到所求.
解答 解:an+1-3an+2an-1=0,即为an+1-an=2(an-an-1),
数列{an-an-1}为首项为1,公比为2的等比数列,
即有an-an-1=2n-2(n>1),
则an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)
=1+1+2+4+…+2n-2=1+$\frac{1-{2}^{n-1}}{1-2}$=2n-1,
则前n项的和Sn=$\frac{1-{2}^{n}}{1-2}$=2n-1.
点评 本题考查等比数列的通项和求和公式的运用,考查数列恒等式的运用及构造数列的思想,属于中档题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
12.数列{an}的通项an=sin$\frac{nπ}{3}$,前n项和为Sn,则S2015等于( )
| A. | $\frac{1}{2}$ | B. | 0 | C. | 1 | D. | -$\frac{1}{2}$ |
13.执行如图所示的程序框图,则输出的S的值为( )


| A. | 1023 | B. | 1024 | C. | 2047 | D. | 2048 |
10.已知函数f(x)=-x2+2ax+1-a在区间[0,1]上的最大值为2,则a的值为( )
| A. | 2 | B. | -1或-3 | C. | 2或-3 | D. | -1或2 |
10.下列命题正确的是( )
| A. | 很大的实数可以构成集合 | |
| B. | 自然数集N中最小的数是1 | |
| C. | 集合{y|y=x2-1}与集合{(x,y)|y=x2-1}是同一个集合 | |
| D. | 空集是任何集合的子集. |
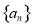 的前
的前 项和为
项和为 ,
, .
. 和
和 ;
; 的前
的前 项和为
项和为 ,证明:
,证明: .
.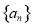 ,
,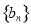 都是等差数列,若
都是等差数列,若 ,则
,则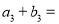 _____________.
_____________.