1.在复平面内,与复数z=-3+4i的共轭复数对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
20.已知集合A={x|x2=x}和集合B={x|lgx≤0},则A∪B等于( )
| A. | (0,1] | B. | (-∞,1] | C. | [0,1) | D. | [0,1] |
19.某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
(Ⅰ)求线性回归方程$\widehat{y}$=bx+a;
(Ⅱ)预计在今后的销售中,销量与单价仍然服从(Ⅰ)中的关系,且该产品的成本是3.5元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本).
(参考公式与数据:$\sum_{i=1}^{6}$xiyi=4066,$\sum_{i=1}^{6}$x${\;}_{i}^{2}$=434.2,$\sum_{i=1}^{6}$xi=51.$\sum_{i=1}^{6}$yi=480.$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.)
| 单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
(Ⅱ)预计在今后的销售中,销量与单价仍然服从(Ⅰ)中的关系,且该产品的成本是3.5元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本).
(参考公式与数据:$\sum_{i=1}^{6}$xiyi=4066,$\sum_{i=1}^{6}$x${\;}_{i}^{2}$=434.2,$\sum_{i=1}^{6}$xi=51.$\sum_{i=1}^{6}$yi=480.$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.)
16. 如图所示,点P在正六边形ABCDEF上按A→B→C→D→E→F→A的路径运动,其中AB=4,则$\overrightarrow{AP}$$•\overrightarrow{AB}$的取值区间为( )
如图所示,点P在正六边形ABCDEF上按A→B→C→D→E→F→A的路径运动,其中AB=4,则$\overrightarrow{AP}$$•\overrightarrow{AB}$的取值区间为( )
 如图所示,点P在正六边形ABCDEF上按A→B→C→D→E→F→A的路径运动,其中AB=4,则$\overrightarrow{AP}$$•\overrightarrow{AB}$的取值区间为( )
如图所示,点P在正六边形ABCDEF上按A→B→C→D→E→F→A的路径运动,其中AB=4,则$\overrightarrow{AP}$$•\overrightarrow{AB}$的取值区间为( )| A. | [-2,6] | B. | [-8,24] | C. | [0,4] | D. | [4,6] |
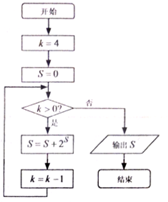
15.某程序框图如图所示,该程序运行后输出的S的值是( )
0 247971 247979 247985 247989 247995 247997 248001 248007 248009 248015 248021 248025 248027 248031 248037 248039 248045 248049 248051 248055 248057 248061 248063 248065 248066 248067 248069 248070 248071 248073 248075 248079 248081 248085 248087 248091 248097 248099 248105 248109 248111 248115 248121 248127 248129 248135 248139 248141 248147 248151 248157 248165 266669

| A. | 2059 | B. | 1035 | C. | 11 | D. | 3 |
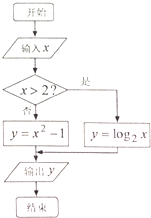 某函数的解析式由如图所示的程序框图给出.
某函数的解析式由如图所示的程序框图给出.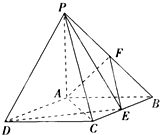 如图所示,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=$\sqrt{3}$,点F是PB的中点,点E在棱BC上移动.
如图所示,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=$\sqrt{3}$,点F是PB的中点,点E在棱BC上移动.