15.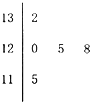 某校高三文,理各两个班在11月份进行了一次质量考试,考生成绩情况如下表所示:已知用分层抽样方法在分数[400,480)的考生中随机抽取27名考生进行质量分析,其中文科考生抽取了7名.(1)求a的值(2)如图是文科不低于550分的5名考生的语文成绩(其中语文满分为150分)的茎叶图,请计算这5名考生的语文成绩的方差;(3)在成绩不低于550分的所有考生中抽取2名进行治疗分析,求至少抽到一名理科生的概率.
某校高三文,理各两个班在11月份进行了一次质量考试,考生成绩情况如下表所示:已知用分层抽样方法在分数[400,480)的考生中随机抽取27名考生进行质量分析,其中文科考生抽取了7名.(1)求a的值(2)如图是文科不低于550分的5名考生的语文成绩(其中语文满分为150分)的茎叶图,请计算这5名考生的语文成绩的方差;(3)在成绩不低于550分的所有考生中抽取2名进行治疗分析,求至少抽到一名理科生的概率.
 某校高三文,理各两个班在11月份进行了一次质量考试,考生成绩情况如下表所示:已知用分层抽样方法在分数[400,480)的考生中随机抽取27名考生进行质量分析,其中文科考生抽取了7名.(1)求a的值(2)如图是文科不低于550分的5名考生的语文成绩(其中语文满分为150分)的茎叶图,请计算这5名考生的语文成绩的方差;(3)在成绩不低于550分的所有考生中抽取2名进行治疗分析,求至少抽到一名理科生的概率.
某校高三文,理各两个班在11月份进行了一次质量考试,考生成绩情况如下表所示:已知用分层抽样方法在分数[400,480)的考生中随机抽取27名考生进行质量分析,其中文科考生抽取了7名.(1)求a的值(2)如图是文科不低于550分的5名考生的语文成绩(其中语文满分为150分)的茎叶图,请计算这5名考生的语文成绩的方差;(3)在成绩不低于550分的所有考生中抽取2名进行治疗分析,求至少抽到一名理科生的概率. | [0,400] | [400,480] | [480,550] | [550,750] | |
| 文科考生 | 67 | 35 | 19 | 5 |
| 理科考生 | 53 | a | 41 | 2 |
9.已知$\overrightarrow{a}$=(4,3),$\overrightarrow{b}$=(-2,1),如果$λ\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{b}$垂直,则|$\overrightarrow{a}$-λ$\overrightarrow{b}$|的值为( )
| A. | 1 | B. | $\sqrt{5}$ | C. | 5 | D. | 2$\sqrt{5}$ |
8.已知sin(π-α)=-2sin($\frac{π}{2}+α$),则$\frac{sinα+cosα}{sinα-cosα}$等于( )
| A. | $\frac{1}{3}$ | B. | 3 | C. | -$\frac{1}{3}$ | D. | -$\frac{2}{3}$ |
7.设a∈[0,4],则使方程x2+ax+1=0有解的概率为( )
0 246581 246589 246595 246599 246605 246607 246611 246617 246619 246625 246631 246635 246637 246641 246647 246649 246655 246659 246661 246665 246667 246671 246673 246675 246676 246677 246679 246680 246681 246683 246685 246689 246691 246695 246697 246701 246707 246709 246715 246719 246721 246725 246731 246737 246739 246745 246749 246751 246757 246761 246767 246775 266669
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
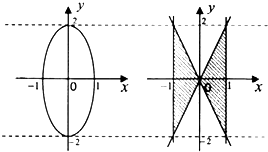 我国齐梁时代的数学家祖恒(公元前5-6世纪)提出了一条原理:“幂势既同,则买家不容异”这句话的意思是:夹在两个平行平面间的两个几何体,被平行于平面的任何平面所截.如果截得的两个截面的面积总是相等,那么这两个几何体的体积相等,设由椭圆x${\;}^{2}+\frac{{y}^{2}}{4}=1$所围成的平面图形绕y轴旋转一周得到的几何体(成为椭球体)体积为V1:由直线y=±2x,x=±1所围成的平面图形(如图阴影部分)绕y轴旋转一周所得到的几何体条件为V2:根据祖恒原理等知识,通过考察V2可得到V1的体积为$\frac{8}{3}π$.
我国齐梁时代的数学家祖恒(公元前5-6世纪)提出了一条原理:“幂势既同,则买家不容异”这句话的意思是:夹在两个平行平面间的两个几何体,被平行于平面的任何平面所截.如果截得的两个截面的面积总是相等,那么这两个几何体的体积相等,设由椭圆x${\;}^{2}+\frac{{y}^{2}}{4}=1$所围成的平面图形绕y轴旋转一周得到的几何体(成为椭球体)体积为V1:由直线y=±2x,x=±1所围成的平面图形(如图阴影部分)绕y轴旋转一周所得到的几何体条件为V2:根据祖恒原理等知识,通过考察V2可得到V1的体积为$\frac{8}{3}π$.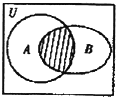 已知集合A={x|1<x<4},集合B={x|x>a},如图中阴影部分表示的集合是C={x|2<x<4},则a的值为( )
已知集合A={x|1<x<4},集合B={x|x>a},如图中阴影部分表示的集合是C={x|2<x<4},则a的值为( )