14.某城市随机监测一年内100天的空气质量PM2.5的数据API,结果统计如下:
(1)若将API值低于150的天气视为“好天”,并将频率视为概率,根据上述表格,预测今年高考6月7日、8日两天连续出现“好天”的概率;
(2)API值对部分生产企业有着重大的影响,假设某企业的日利润f(x)与API值x的函数关系为:f(x)=$\left\{\begin{array}{l}40(x≤150)\\ 15(x>150)\end{array}$(单位;万元),利用分层抽样的方式从监测的100天中选出10天,再从这10天中任取3天计算企业利润之和X,求离散型随机变量X的分布列以及数学期望和方差.
0 246438 246446 246452 246456 246462 246464 246468 246474 246476 246482 246488 246492 246494 246498 246504 246506 246512 246516 246518 246522 246524 246528 246530 246532 246533 246534 246536 246537 246538 246540 246542 246546 246548 246552 246554 246558 246564 246566 246572 246576 246578 246582 246588 246594 246596 246602 246606 246608 246614 246618 246624 246632 266669
| API | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,+∞) |
| 天数 | 6 | 12 | 22 | 30 | 14 | 16 |
(2)API值对部分生产企业有着重大的影响,假设某企业的日利润f(x)与API值x的函数关系为:f(x)=$\left\{\begin{array}{l}40(x≤150)\\ 15(x>150)\end{array}$(单位;万元),利用分层抽样的方式从监测的100天中选出10天,再从这10天中任取3天计算企业利润之和X,求离散型随机变量X的分布列以及数学期望和方差.
 如图AB是圆O的一条弦,过点A作圆的切线AD,作BD⊥AD,与该圆交于点E,若AD=2$\sqrt{3}$,DE=2.
如图AB是圆O的一条弦,过点A作圆的切线AD,作BD⊥AD,与该圆交于点E,若AD=2$\sqrt{3}$,DE=2.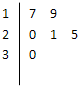 某车间共有12名工人,随机抽取6名作为样本,他们某日加工零件的个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.
某车间共有12名工人,随机抽取6名作为样本,他们某日加工零件的个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.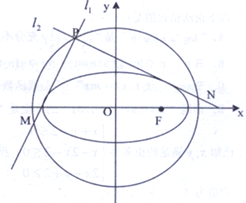 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点F($\sqrt{2}$,0)其短轴上的一个端点到F的距离为$\sqrt{3}$
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点F($\sqrt{2}$,0)其短轴上的一个端点到F的距离为$\sqrt{3}$