3.已知在直角梯形ABCD中,AB∥CD,AB⊥AD,AB=AD=2,CD=1,P为线段BC上一个动点,设$\overrightarrow{BP}=λ\overrightarrow{BC}$,则当$\overrightarrow{PA}•\overrightarrow{PD}$取得最小值时λ的值是( )
| A. | $\frac{1}{2}$ | B. | $\frac{4}{5}$ | C. | 0 | D. | 1 |
2.已知函数f(x)是定义在R上的奇函数,且在区间[0,+∞)上单调递增,若a,b均为不等于1的正实数,则a>b是$f(\frac{1}{{{{log}_a}2}})+f({log_{\frac{1}{2}}}b)>0$成立的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
1.已知抛物线y2=4x与双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1(a>0,b>0)$的一条渐近线交于点M(M异于原点),且点M到抛物线焦点的距离等于3,则双曲线的离心率是( )
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\frac{{\sqrt{6}}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
20.将$y=sin(2x-\frac{π}{4})$的图象上所有点向左平移$\frac{π}{4}$后得到y=f(x)的图象,则y=f(x)在[-$\frac{π}{2}$,0]上的最小值为( )
| A. | -1 | B. | $-\frac{{\sqrt{2}}}{2}$ | C. | 0 | D. | $-\frac{{\sqrt{3}}}{2}$ |
17.已知函数f(x)=x2+bx+c,(b,c∈R),集合A={x丨f(x)=0},B={x|f(f(x))=0},若存在x0∈B,x0∉A则实数b的取值范围是( )
0 245937 245945 245951 245955 245961 245963 245967 245973 245975 245981 245987 245991 245993 245997 246003 246005 246011 246015 246017 246021 246023 246027 246029 246031 246032 246033 246035 246036 246037 246039 246041 246045 246047 246051 246053 246057 246063 246065 246071 246075 246077 246081 246087 246093 246095 246101 246105 246107 246113 246117 246123 246131 266669
| A. | 0≤b≤4 | B. | b≤0或 b≥4 | C. | 0≤b<4 | D. | b<0或b≥4 |
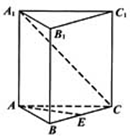 如图,已知正三棱柱ABC-A1B1C1的各棱长均相等,E是BC的中点,点F在侧棱CC1上,且CC1=4CF
如图,已知正三棱柱ABC-A1B1C1的各棱长均相等,E是BC的中点,点F在侧棱CC1上,且CC1=4CF 如图,边长为$\sqrt{2}$的正方形ADEF与梯形ABCD所在的平面互相垂直,其中AB∥CD,AB⊥BC,DC=BC=$\frac{1}{2}$AB=1,点M在线段EC上.
如图,边长为$\sqrt{2}$的正方形ADEF与梯形ABCD所在的平面互相垂直,其中AB∥CD,AB⊥BC,DC=BC=$\frac{1}{2}$AB=1,点M在线段EC上.