题目内容
15. 如图,边长为$\sqrt{2}$的正方形ADEF与梯形ABCD所在的平面互相垂直,其中AB∥CD,AB⊥BC,DC=BC=$\frac{1}{2}$AB=1,点M在线段EC上.
如图,边长为$\sqrt{2}$的正方形ADEF与梯形ABCD所在的平面互相垂直,其中AB∥CD,AB⊥BC,DC=BC=$\frac{1}{2}$AB=1,点M在线段EC上.(Ⅰ)证明:平面BDM⊥平面ADEF;
(Ⅱ)判断点M的位置,使得平面BDM与平面ABF所成锐二面角为$\frac{π}{3}$.
分析 (Ⅰ)由已知三角形的半径关系得到AD⊥BD,再由面面垂直的性质得到ED⊥面ABCD,进一步得到BD⊥ED,利用线面垂直的判定得到BD⊥面ADEF,由BD?面BDM,利用面面垂直的判定得到平面BDM⊥平面ADEF;
(Ⅱ)在面DAB内过D作DN⊥AB,垂足为N,则可证得DN⊥CD,以D为坐标原点,DN所在直线为x轴,DC所在直线为y轴,DE所在直线为z轴,建立空间直角坐标系,求出所用点的坐标,结合E,M,C三点共线得到$\overrightarrow{EM}=λ\overrightarrow{EC}(0<λ<1)$,把M的坐标用含有λ的代数式表示,求出平面BDM的法向量,再由平面ABF的法向量为$\overrightarrow{{n}_{2}}=\overrightarrow{DN}=(1,0,0)$,由平面BDM与平面ABF所成锐二面角为$\frac{π}{3}$求得$λ=\frac{2}{3}$.则点M的坐标可求,位置确定.
解答 (Ⅰ)证明:如图,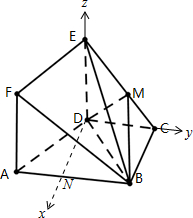 ∵DC=BC=1,DC⊥BC,∴BD=$\sqrt{2}$,
∵DC=BC=1,DC⊥BC,∴BD=$\sqrt{2}$,
又∵AD=$\sqrt{2}$,AB=2,∴AD2+BD2=AB2,则∠ADB=90°,
∴AD⊥BD.
又∵面ADEF⊥面ABCD,ED⊥AD,面ADEF∩面ABCD=AD,
∴ED⊥面ABCD,则BD⊥ED,
又∵AD∩DE=D,∴BD⊥面ADEF,又BD?面BDM,
∴平面BDM⊥平面ADEF;
(Ⅱ)在面DAB内过D作DN⊥AB,垂足为N,
∵AB∥CD,∴DN⊥CD,
又∵ED⊥面ABCD,∴DN⊥ED,
∴以D为坐标原点,DN所在直线为x轴,DC所在直线为y轴,DE所在直线为z轴,建立空间直角坐标系,
∴B(1,1,0),C(0,1,0),E(0,0,$\sqrt{2}$),N(1,0,0),
设M(x0,y0,z0),由$\overrightarrow{EM}=λ\overrightarrow{EC}(0<λ<1)$,得$({x}_{0},{y}_{0},{z}_{0}-\sqrt{2})=λ(0,1,-\sqrt{2})$,
∴x0=0,${y}_{0}=λ,{z}_{0}=\sqrt{2}(1-λ)$,则M(0,λ,$\sqrt{2}(1-λ)$),
设平面BDM的法向量$\overrightarrow{{n}_{1}}=(x,y,z)$,则$\left\{\begin{array}{l}{\overrightarrow{{n}_{1}}•\overrightarrow{DM}=0}\\{\overrightarrow{{n}_{1}}•\overrightarrow{DB}=0}\end{array}\right.$,∴$\left\{\begin{array}{l}{λy+\sqrt{2}z(1-λ)=0}\\{x+y=0}\end{array}\right.$,
令x=1,得$\overrightarrow{{n}_{1}}=(1,-1,\frac{λ}{\sqrt{2}(1-λ)})$.
∵平面ABF的法向量$\overrightarrow{{n}_{2}}=\overrightarrow{DN}=(1,0,0)$,
∴$cos<\overrightarrow{{n}_{1}},\overrightarrow{{n}_{2}}>=\frac{1}{\sqrt{1+1+\frac{{λ}^{2}}{2(1-λ)^{2}}}}=\frac{1}{2}$,解得:$λ=\frac{2}{3}$.
∴M(0,$\frac{2}{3},\frac{\sqrt{2}}{3}$),
∴点M的位置在线段CE的三等分点且靠近C处.
点评 本题主要考查直线与平面之间的平行、垂直等位置关系,二面角的概念、求法等知识,以及空间想象能力和逻辑推理能力,训练了利用空间向量求二面角的平面角,是中档题.

| A. | -1 | B. | $-\frac{{\sqrt{2}}}{2}$ | C. | 0 | D. | $-\frac{{\sqrt{3}}}{2}$ |
| A. | 9 | B. | 16 | C. | 21 | D. | 11 |
 如图,平面ABCD⊥平面PAB,且四边形ABCD为正方形,△PAB为正三角形,M为PD的中点,E为线段BC上的动点.
如图,平面ABCD⊥平面PAB,且四边形ABCD为正方形,△PAB为正三角形,M为PD的中点,E为线段BC上的动点.