题目内容
【题目】已知函数![]() .
.
(1)若![]() ,求曲线
,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)求函数![]() 的单调区间;
的单调区间;
(3)若![]() 且
且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]()
【解析】
(1)代入![]() ,再根据导数的几何意义求解即可.
,再根据导数的几何意义求解即可.
(2)易得![]() ,因为
,因为![]() ,故分
,故分![]() 与
与![]() 两种情况分析导数的正负,从而得出单调区间即可.
两种情况分析导数的正负,从而得出单调区间即可.
(3)根据(2)中的单调性,分![]() 与
与![]() 两种情况讨论
两种情况讨论![]() 的单调性,并求出最值,再根据
的单调性,并求出最值,再根据![]() 的值域满足的关系结合题意求解即可.
的值域满足的关系结合题意求解即可.
(1)若![]() ,则
,则![]() ,故
,故![]() ,
,![]() ,
,![]() ,
,
∴所求切线方程为![]() ;
;
(2)函数的定义域为![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上单调递减,
上单调递减,
当![]() 时,令
时,令![]() 得
得![]() ,令
,令![]() 得
得![]() ,故函数
,故函数![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增;
单调递增;
(3)当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减,
上单调递减,
又 ,而
,而![]() ,不合题意;
,不合题意;
当![]() 时,由(2)可知,
时,由(2)可知,![]() ,
,
(i)当![]() ,即
,即![]() 时,
时,![]() ,不合题意;
,不合题意;
(ii)当![]() ,即
,即![]() 时,
时,![]() ,满足题意;
,满足题意;
(iii)当![]() ,即
,即![]() 时,则
时,则![]() ,
,
∵![]() ,函数
,函数![]() 在
在![]() 单调递增,
单调递增,
∴当![]() 时,
时,![]() ,
,
又∵函数的定义域为![]() ,
,
∴![]() ,满足题意.
,满足题意.
综上,实数![]() 的取值范围为
的取值范围为![]() .
.

【题目】在某外国语学校举行的![]() (高中生数学建模大赛)中,参与大赛的女生与男生人数之比为
(高中生数学建模大赛)中,参与大赛的女生与男生人数之比为![]() ,且成绩分布在
,且成绩分布在![]() ,分数在
,分数在![]() 以上(含
以上(含![]() )的同学获奖.按女生、男生用分层抽样的方法抽取
)的同学获奖.按女生、男生用分层抽样的方法抽取![]() 人的成绩作为样本,得到成绩的频率分布直方图如图所示.
人的成绩作为样本,得到成绩的频率分布直方图如图所示.
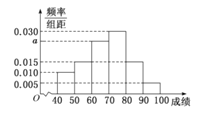
(Ⅰ)求![]() 的值,并计算所抽取样本的平均值
的值,并计算所抽取样本的平均值![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(Ⅱ)填写下面的![]() 列联表,并判断在犯错误的概率不超过
列联表,并判断在犯错误的概率不超过![]() 的前提下能否认为“获奖与女生、男生有关”.
的前提下能否认为“获奖与女生、男生有关”.
女生 | 男生 | 总计 | |
获奖 |
| ||
不获奖 | |||
总计 |
| ||
附表及公式:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中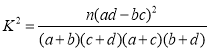 ,
,![]() .
.
【题目】“工资条里显红利,个税新政人民心”我国自1980年以来,力度最大的一次个人所得税(简称个税)改革迎来了全面实施的阶段.2019年1月1日实施的个税新政主要内容包括:(1)个税起征点为5000元;(2)每月应纳税所得额(含税)![]() 收人
收人![]() 个税起征点
个税起征点![]() 专项附加扣除;(3)专项附加扣除包括住房、子女教育和赡养老人等.新旧个税政策下每月应纳税所得额(含税)计算方法及其对应的税率表如下:
专项附加扣除;(3)专项附加扣除包括住房、子女教育和赡养老人等.新旧个税政策下每月应纳税所得额(含税)计算方法及其对应的税率表如下:
旧个税税率表(个税起征点3500元) | 新个税税率表(个税起征点5000元) | |||
缴税基数 | 每月应纳税所得额(含税) | 税率(%) | 每月应纳税所得额(含税) | 税率(%) |
1 | 不超过1500元的部分 | 3 | 不超过3000元的部分 | 3 |
2 | 超过1500元至4500元的部分 | 10 | 超过3000元至12000元的部分 | 10 |
3 | 超过4500元至9000元的部分 | 20 | 超过12000元至25000元的部分 | 20 |
4 | 超过9000元至35000元的部分 | 25 | 超过25000元至35000元的部分 | 25 |
5 | 超过35000元至55000元的部分 | 30 | 超过35000元至55000元的部分 | 30 |
… | … | … | … | … |
随机抽取某市2020名同一收入层级的![]() 从业者的相关资料,经统计分析,预估他们2019年的人均月收入24000元,统计资料还表明,他们均符合住房专项扣除;同时,他们每人至多只有一个符合子女教育扣除的孩子,并且他们中既不符合子女教育扣除又不符合赡养老人扣除、只符合子女教育扣除但不符合赡养老人扣除、只符合赡养老人扣除但不符合子女教育扣除、既符合子女教育扣除又符合赡养老人扣除的人数之比是
从业者的相关资料,经统计分析,预估他们2019年的人均月收入24000元,统计资料还表明,他们均符合住房专项扣除;同时,他们每人至多只有一个符合子女教育扣除的孩子,并且他们中既不符合子女教育扣除又不符合赡养老人扣除、只符合子女教育扣除但不符合赡养老人扣除、只符合赡养老人扣除但不符合子女教育扣除、既符合子女教育扣除又符合赡养老人扣除的人数之比是![]() ;此外,他们均不符合其他专项附加扣除,新个税政策下该市的专项附加扣除标准为:住房1000元/月,子女教育每孩1000元/月,赡养老人2000元/月等.假设该市该收入层级的
;此外,他们均不符合其他专项附加扣除,新个税政策下该市的专项附加扣除标准为:住房1000元/月,子女教育每孩1000元/月,赡养老人2000元/月等.假设该市该收入层级的![]() 从业者都独自享受专项附加扣除,将预估的该市该收入层级的
从业者都独自享受专项附加扣除,将预估的该市该收入层级的![]() 从业者的人均月收入视为其个人月收入,根据样本估计总体的思想,解决如下问题:
从业者的人均月收入视为其个人月收入,根据样本估计总体的思想,解决如下问题:
(1)求在旧政策下该收入层级的![]() 从业者每月应纳的个税;
从业者每月应纳的个税;
(2)设该市该收入层级的![]() 从业者2019年月缴个税为X元,求X的分布列和期望;
从业者2019年月缴个税为X元,求X的分布列和期望;
(3)根据新旧个税方案,估计从2019年1月开始,经过多少个月,该市该收入层级的![]() 从业者各月少缴纳的个税之和就超过2019年的人均月收入?
从业者各月少缴纳的个税之和就超过2019年的人均月收入?