题目内容
【题目】已知数列![]() 的前
的前![]() 项积为
项积为![]() ,即
,即![]() .
.
(1)若数列![]() 为首项为2016,公比为
为首项为2016,公比为![]() 的等比数列,
的等比数列,
①求![]() 的表达式;②当
的表达式;②当![]() 为何值时,
为何值时, ![]() 取得最大值;
取得最大值;
(2)当![]() 时,数列
时,数列![]() 都有
都有![]() 且
且![]() 成立,
成立,
求证: ![]() 为等比数列.
为等比数列.
【答案】(1)① ;②12;(2)见解析.
;②12;(2)见解析.
【解析】试题分析:
(1)①由题意知![]() ,则
,则![]() ,化简可得结论;②记
,化简可得结论;②记![]() ,
,![]() ,即
,即![]() ,
,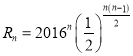 ,作商
,作商![]() ,计算出
,计算出![]() 的最大值,再由n是奇数时,
的最大值,再由n是奇数时, ![]() 负数,n是偶数时,
负数,n是偶数时, ![]() 是正数,即可得出结论;
是正数,即可得出结论;
(2) 当![]() 时, 易得
时, 易得![]() ;由
;由![]() 得,当
得,当![]() 时,
时, ![]() ,两式相除,化简可得
,两式相除,化简可得![]() ,可得
,可得![]() ,这两式相除,则易得结论.
,这两式相除,则易得结论.
试题解析:
(1)①由题意知![]() ,
,
所以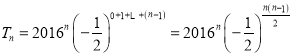
②记![]() ,
,![]() ,即
,即![]() ,
,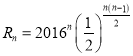 ,
,
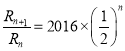 ,当
,当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,
,
又因为![]() ,所以,当
,所以,当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,所以
,所以![]() 的最大值为
的最大值为![]()
此时![]() ,而
,而![]() ,所以
,所以![]() .
.
而 ,
,
所以,当![]() 时,
时, ![]() 取得最大值
取得最大值
(2)当![]() 时,
时, ![]() ,所以
,所以![]() ,即
,即![]() ,
,
已知![]() ①
①
当![]() 时,
时, ![]()
①②两式相除得![]() ,化简得
,化简得![]() ,③
,③
又因为![]() ,④
,④
③两式相除得![]() ,⑤
,⑤
⑤式可化为: 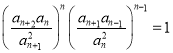 ,
, ![]()
令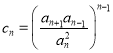 ,所以
,所以![]() ,所以
,所以![]() ,
,
即![]() ,
,![]() 都成立,
都成立,
所以![]() 为等比数列.
为等比数列.

练习册系列答案
相关题目